2.Workfileの作成 EViewsでは一連の分析をインタラクティブ・モードあるいはバッチ・モード(処理手順をプログラム化し、一括で処理を行う方法)で行うことができますが、以下ではインタラクティブ・モードで分析を行う場合について説明します。 EViewsで入力作業を行うときの注意
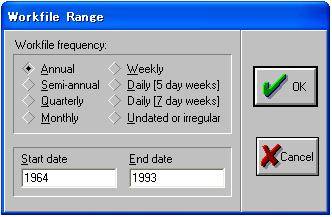
手順2 図3の「Workfile Range」ウインドウが開くので、必要事項を入力する。
「Workfile frequency」欄は、データの周期を指定するもので、適切なボタンをクリックします。各ボタンの意味は、
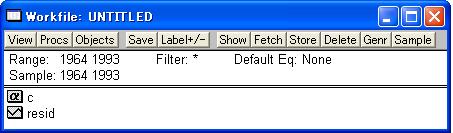
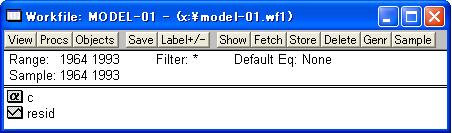
ここでの例の場合は年次データですので「Annual」をクリックします。 なお、クロスセクションデータあるいはパネルデータの場合は「undated or irregular」を選び、「start date」に1、「end date」にデータ数を入力します。時系列データで年次データ以外の場合は4 桁の西暦表現と四半期・月等の期数をコロン(:)で区切って入力します。月次データで2008年12月は「2008:12」となります。 次に「OK」ボタンをクリックすると、図4の「Workfile」ウインドウが開きます。なお、変数名欄の「c」は定数、「resid」は残差を意味し、これらは固定された変数名であり常に表示されます。
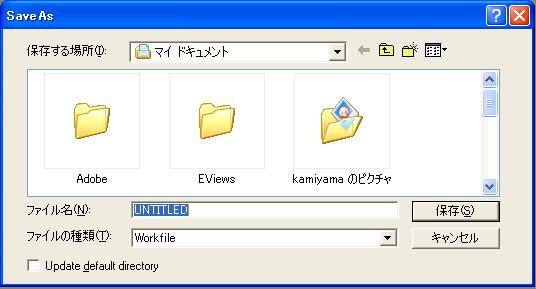
手順3 Workfileに名前をつけて保存する。 Workfileウインドウの「Save」ボタンをクリックすると、図5のような「SaveAs」ウインドウが現れるので、
とし、さらに 左下のボックス(Update default directory)にチェックをつけて(このことはファイルを保存するフォルダを固定することを意味する。)、「保存」ボタンをクリックします。その結果、図6のように「Workfile」ウィンドウのタイトルが「MODEL-01」に変更されます。
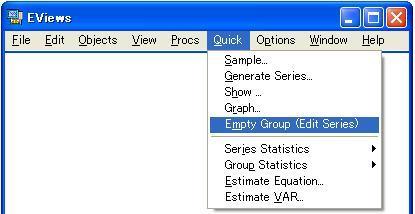
3.ExcelからEViewsへのデータ入力 手順1 EViewsのスプレッドシートを開く EViewsのメインメニューから図7のようにQuick/Empty Group (Edit Series)を選択すると、
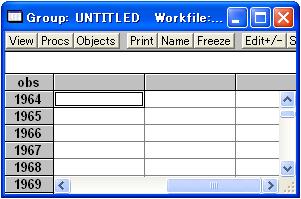
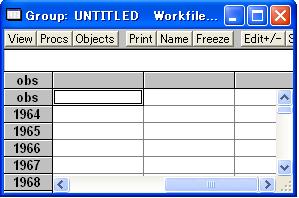
図8のようにEViewsのスプレッドシートが開きます。 手順2 EViewsスプレッドシートのセル「obs」をアクティブにする キーボードの矢印キー(↑)を押して、アクティブセルを1行上方へ移動させ、図9のように「obs」という名前の行が見えるようにします。「obs」は、データ名の入力欄を意味します。
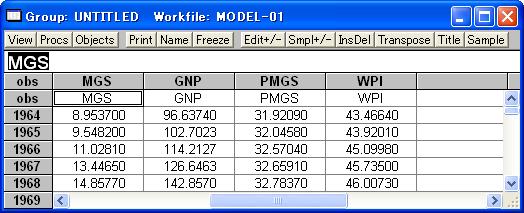
手順3 Excelデータのコピー 表1のようにデータが入力されているとき、セルB1からセルE31を範囲指定し、「コピー(Ctrl+cを押すか、マウスで右クリックして「コピー」を選択する。)」する。 手順4 EViewsのスプレッドシートへのペースト EViewsのウィンドウをアクティブにし、図9のような状態にする。このとき、EViewsのタイトルバーをクリックし、スプレッドシート上のセルをクリックしない方がよいでしょう。Ctrl+vを押して、Excelからクリップボードにコピーされたデータをペースト(貼り付け)する。その結果、図10のようにEViewsのスプレッドシートにデータが入力される。
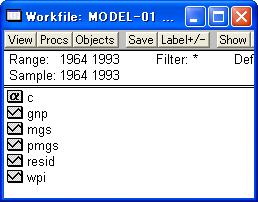
さらに、図11のように、EViewsのWorkfileに、入力されたデータの系列名が追加される。
ここで注意すべきことは、EViewsではデータがスプレッドシートではなくWorkfileに保存されており、スプレッドシートに表示されるデータを修正すると、自動的にWorkfileに保存されているデータも修正されることである。 手順5 スプレッドシートを閉じる EViewsのスプレッドシートの右上の×印をクリックする。警告メッセージが出るので、「Yes」を選択すればスプレッドシートが閉じます。なお、データはすべてWorkfileに保存されており、スプレッドシートはそのデータを表示したり修正するためのものであり、×印でスプレッドシートを閉じてもデータが失われるわけではない。
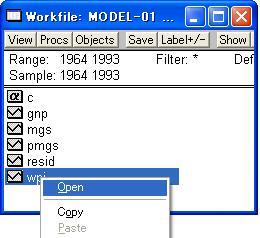
4.データの表示(一変数のみを表示する場合) 表示したい系列1個(ここでは「WPI」とします)を右クリックし、図12のように表示されるメニューから「Open」を選択すると、図13のような画面が表示されます。
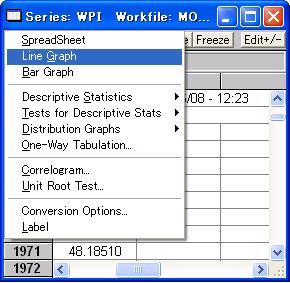
この例では系列WPIを選択しましたので、タイトルのSeries名が「WPI」となっています。当初、データはスプレッドシート形式で表示されますが、Seriesウインドウの「View」ボタンをクリックしたときに表示されるプルダウンメニュー(図14)の項目を選ぶことで、スプレッドシート形式以外の表示を選ぶことができます。それらは
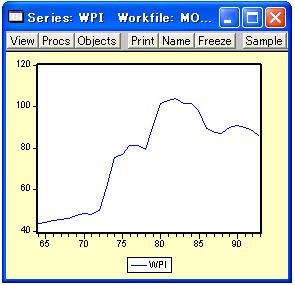
であり、その他にも選択された系列に関する各種統計値を表示するための項目があります。例えばDescriptive Statistics/Histogram and Statsを選択すれば系列のヒストグラムと基本統計量を表示することができます。 図14のように「Line Graph」を選択すると、図15のように選択された系列が折れ線グラフで表示されます。
5.データの表示(複数の変数を表示する場合) Workfileウインドウで、Ctrlキーを押しながら系列名をクリックすることで、図16のように複数の変数を選択することができます。
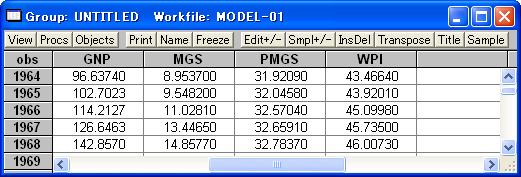
選択した部分の上で右クリックし、図17のようにOpen/as Groupを選択すると、図18のように「Group」ウインドウが開き、選択した全系列がスプレッドシート形式で表示されます。
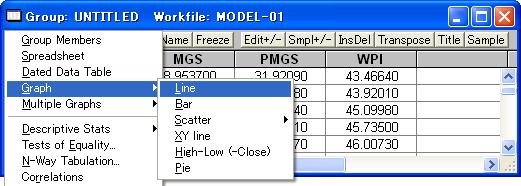
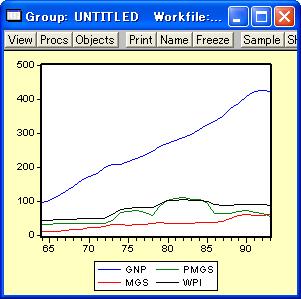
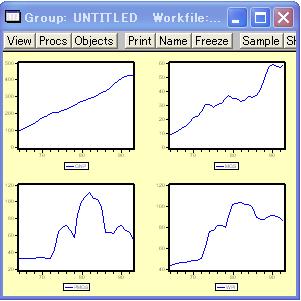
「Group」ウインドウの「View」ボタンをクリックし、図19のようにGraph/Lineを選択すれば図20、Multiple Graphs/Lineを選択すれば図21の折れ線グラフ表示することができます。
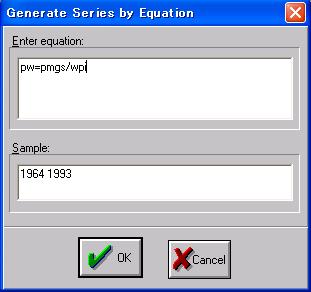
6.データの加工 EViewsでは、Workfileに保存されている系列のデータを加工し、新たな系列を作成することができます。ここでは、既にWorkfile上には系列 PMGSと系列WPIがありますので、これらを使って新しい系列PW=PMGS/WPIを作成する方法を説明します。 手順1 Workfileウインドウの「Genr」ボタンをクリックすれば、「Generate Series by Equarion」ウインドウが開きます。 手順2 「Generate Series by Equarion」ウインドウの「Enter equation」欄に図22のように計算式を入力し、「OK」ボタンをクリックすれば系列PWの作成が完了します。
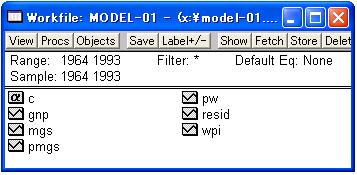
その結果、図23のようにWorkfileに系列PWが追加されます。
「Enter equation」欄に入力する計算式は『新たな系列名=数式』のような形式にしなければなりません。 【数式の例】 系列GNPの中心化4項移動平均を系列GNP_MA4として作成するためには、「Genr」ボタンをクリックし、「Generate Series by Equarion」ウインドウの「Enter equation」欄に
と入力し、「OK」ボタンをクリックすれば系列GNP_MA4が作成されます。この例で示すようにEViewsでは、1期前のデータをGNP(-1)で表現し、1期後のデータをGNP(1)で表現します。 【数式で使える主な関数】 EViewsでは次の関数が用意されています。
系列MGS、GNP、PWの自然対数系列ln_MGS、ln_GNP、ln_PWを作成します。計算式は
ですので、各自作成してみて下さい。
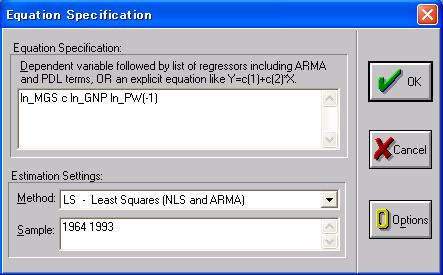
7.最小2乗法によるモデルの推計 推計方法には、単一方程式推定法(モデル式を1本ずつ推計する方法)と、連立方程式推定法(モデルが複数の式で構成されているときモデル全体を一度に推計する方法)がありますが、ここでは単一方程式推定法のみを説明します。 単一方程式推定法には、OLS(Ordinary Least Square:最小2乗法)、2SLS(2 Stage Least Square:2段階最小2乗法)とLIML(Limited Information Maximum Likelihood:制限情報最尤法)がありますが、ここではOLSのみを説明します。 EViewsのメインメニューから、Quick/Estimate Equationを選択すると、図24の「Equation Specification」ウインドウが表示されます。「Equation Specification:」欄は「推定式」を入力すべき場所であり、「Method:」欄は「推定方法」を選択するためのものであり、「Sample:」欄は「推定に使用するデータのサンプル期間」を指定するところです。
「Equation Specification:」欄に記入すべき「推定式」は、=や+の記号および係数は書かなくても意味がわかることから省略することとなっております。したがって、Workfileに保存されている系列の名前のみで表現することになります。 図24の場合は、元々のモデル
を、保存した系列名で表現し直した
なる推定式を
と記述しています。なお、ln_PW(-1)は先にも説明したように系列ln_PWの1期前の値を使うことを意味しています。 別の例として
なるモデルを推計するときの「推定式」は
となり、(X1 + X2) はX1とX2の和を1変数として扱うことを意味します。このように「推定式」に計算式を使用することも可能であり、推定式(6-3)は
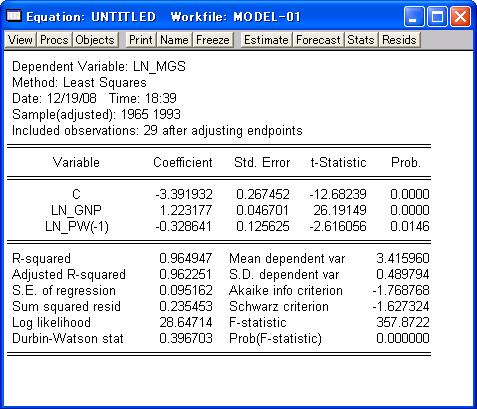
と記述することも可能です。すなわち、系列ln_MGS、ln_GNP、ln_PWを作成しなくてもよいことを意味します。 「Method:」欄のデフォルトは「LS」すなわち「最小2乗法」であるので変更しません。さらに、「Sample:」欄には保存されているデータ期間のすべてを使用するものとして「1964 1993」が表示されるので変更しません。保存されているデータ期間の一部のみを推計に使用する場合は変更します。必要事項を入力した後、「OK」ボタンをクリックすると、図25のように「Equation」ウインドウによって推計結果が表示されます。
ここで、各項目の意味は次のようになります。
なお、この例の場合、図24では「Sample:」を「1964 1993」としたのに図25の「Sample(adjusted):」が「1965 1993」となっているのは、モデル式にln PW-1が含まれており、lnPWの1963年の値がないためln MGSの1964年のデータが使えなかったことによります。 【残差に系列相関が存在する場合の対処法】 図25の推定結果によれば、「Durbin-Watson stat」が0.3967であり、残差に正の系列相関が存在することになり、推定結果を使用することができません。 系列相関を除去する手法は、コクランオーカット法が一般的ですが、EViewsでは説明変数の最後に「AR(1)」を加えることで対応します。AR(1)は、1次の自己回帰項と呼ばれるものであります。 「Equation Specification:」欄に
と入力することは
なるモデルを推計することになり、AR(1)を追加した
と入力することは
すなわち
なるモデルを推計することになります。モデル(6-3)の推計で得られた残差etから
を満たすρを推計し、
として
なるモデルを推計する一般的なコクランオーカット法とモデル(6-5)を推計した場合の違いは
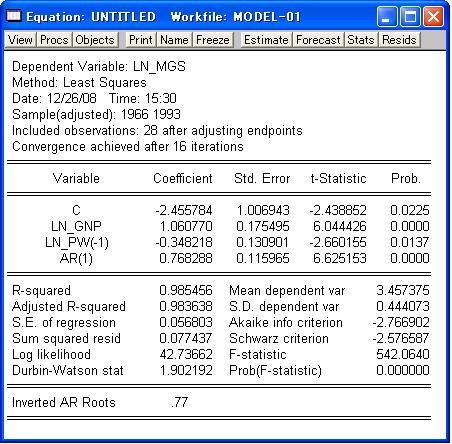
となることだけであり、AR(1)を追加だけでコクランオーカット法が適用されたこととなります。 図25の「Equation」ウインドウの「Estimate」ボタンをクリックすると、図24の「Equation Specification」ウインドウが再表示され、設定を変更して再計算することができるようになります。説明変数の最後に「AR(1)」を加え「OK」ボタンをクリックすると、図26のような推計結果が得られます。図25と図26を比較すると、コクランオーカット法を適用したため「Sample(adjusted):」の始期が1年遅れて1966となり、データ数が1つ減っています。さらに、「Variable」に「AR(1)」が追加されます。この系列AR(1)の係数0.768288がρの推計値となります。
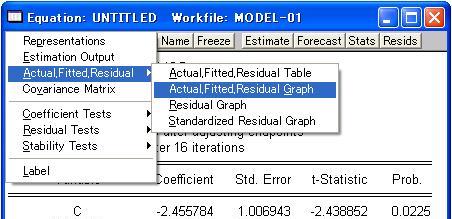
モデル(6-5)を見れば、推計すべきパラメータとしてρc、β1ρ、β2ρがあり、非線形最小2乗法による推計が必要となります。この推計は、収束計算によって行われるため、図26では「Convergence achieved after 16 iterations」の表示が追加されており、16回の繰り返しで計算が行われたことが示されています。なお、INVERTED AR Rootsは、反転可能性条件が満たされていたかどうかを示すもので、その値が1に近いときは反転不能であり、AR(1)を追加したモデルが不適切であったことになる。反転不能であった場合は「Estimated AR process is noninvertible」と表示されます。 「Equation」ウインドウの「View」ボタンをクリックすると、図27のように推計結果の表示形式を変更するための選択項目が表示される。「Estimation Output」は図26のような表示形式のためのものであり、「Representations」は推計結果を数式表示するためのもので、各種データを表示するのが「Actual, Fitted, Residual」である。さらに、「Covariance Matrix」は推計に使用した系列間の共分散を表示するためのものである。この共分散をチェックすることで「多重共線性」の有無を概観することができます。
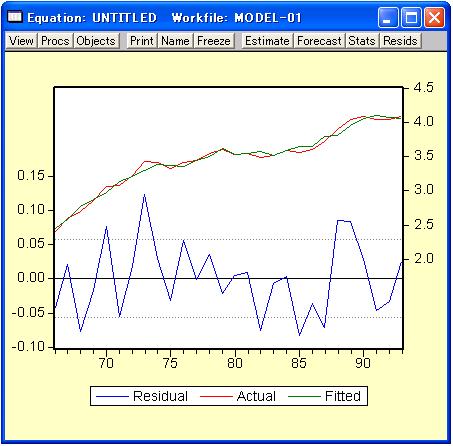
図27のように「Actual, Fitted, Residual」の「Actual, Fitted, Residual Graph」を選択すると、図28のように「Residual(残差)」、「Actual(被説明変数)」、「Fitted(被説明変数のモデルによる推定値)」、がグラフ表示されます。ここで、「Residual」は左目盛りであり、「Actual」と「Fitted」は右目盛りになります。ちなみに、Actual = Fitted + Residualという関係があります。
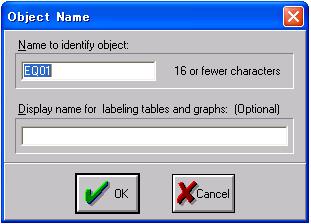
「Equation」ウインドウの「Name」ボタンをクリックすることで推計結果を「Workfile」に保存することができる。「Name」ボタンをクリックすると、図29のように「Object Name」ウインドウが表示され、「Name to identity object:」欄に推計結果に付ける名前の入力が求められます。名前は16文字以内の英数半角入力でなければならず、特殊文字(%、/、$等)は利用できません。
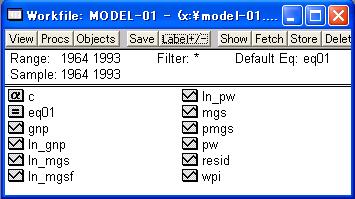
「Display name for labeling tables and graphs:」欄はより詳細な推計内容を記述するためのものであり、記述しなくてもかまいません。ここに入力した情報は、「Workfile」ウインドウのメニューにある「Label+/-」ボタンをクリックすることで表示/非表示を切り替えることができます。 ここでは、図29のように「EQ01」という名前を付けて保存することとし、「OK」ボタンをクリックする。すると、図30のように系列名リストの中に「eq01」という項目が追加される。このように推計結果は各系列と同様な形で保存されます。
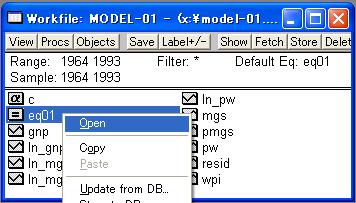
図31のように推計結果名を右クリックし、「Open」を選択すれば、推計結果を再表示することができる。
|
| (2009年1月20日作成) |