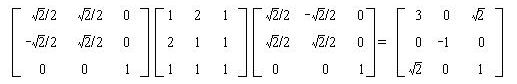実対称行列の固有値計算マクロ
実対称行列(要素がすべて実数である対称行列)の固有値はすべて実数であること、行列Aの固有値
は、任意の正則行列JによってJAJ-1と(相似)変換した行列の固有値と一致すること、対角行列の
固有値はその各対角要素であることが知られている。ここではヤコビ法と呼ばれる反復計算方法で、実
対称行列の固有値の近似値を求めるアルゴリズムを説明する。
【手順1】
行列Aの非対角要素で絶対値が最大な要素を見つける。それがA(i,j)=A(j,i)であったものと
し、その値が許容される値よりも小さいときは反復計算を終了し手順5へ進み、さもないときは手
順2へ進む。ただし、A(i,j)は行列Aの上からi行目、左からj列目の要素を意味する。許容さ
れる値としては、ほとんど 0 とみなすことができる値(例えば10-10)を設定する。
【手順2】
回転角θを次式により求める。
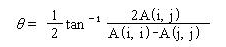 【手順3】
単位行列で、(i,i)要素と(j,j)要素をcosθ、(i,j)要素をsinθ、(j,i)要素を-sinθに置き換えた
回転行列Jを考える。回転行列JはJ-1=JTという性質を持っている。
【手順4】
相似変換JAJ-1=JAJTを求め、その結果を新たなAとして手順1へ戻る。
【手順5】
非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみなすこ
とができ、各対角要素が固有値となる。
【手順3】
単位行列で、(i,i)要素と(j,j)要素をcosθ、(i,j)要素をsinθ、(j,i)要素を-sinθに置き換えた
回転行列Jを考える。回転行列JはJ-1=JTという性質を持っている。
【手順4】
相似変換JAJ-1=JAJTを求め、その結果を新たなAとして手順1へ戻る。
【手順5】
非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみなすこ
とができ、各対角要素が固有値となる。
【例題】
次の実対称行列の固有値を考える。
 非対角要素で絶対値最大なものはA(1, 2)=A(2, 1)=2 であるから、回転角θは
非対角要素で絶対値最大なものはA(1, 2)=A(2, 1)=2 であるから、回転角θは
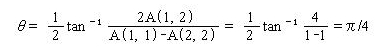
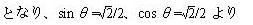
 相似変換は
相似変換は
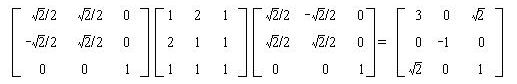 となる。得られた行列の非対角要素は0とみなせないので、さらに操作を繰り返さなければならない。
となる。得られた行列の非対角要素は0とみなせないので、さらに操作を繰り返さなければならない。
右図のように固有値を求める行列(この例では3×3行列)を入力し、
1−1要素の上のセルに行列の大きさ(この例では3)を記し、そのセ
ルをアクティブにして実行したとき固有値を◇の場所に出力するマクロ
を作成しなさい。計算手順は先に配布したヤコビ法によるものとする。
【手順0−1】行列の大きさを読み込み、配列を用意する
行列の大きさのセルがアクティブであるので、変数nに読み込むこ
とにし、データを保存する配列を用意する。
n = ActiveCell
ReDim A(n, n), B(n, n), C(n, n)
|
| 3 | | |
| 1 | 2 | 1 |
| 2 | 1 | 1 |
| 1 | 1 | 1 |
| | | |
| ◇ | ◇ | ◇ |
|
【手順0−2】データを読み込む
すべてのデータを配列Aに読み込むためには、「アクティブセルを1つ下げて、右へn個読
み込み、一番左へ戻る。」操作をn回繰り返せばよいことになる。
For i = 1 To n
ActiveCell.Offset(1, 0).Range("A1").Select
For j = 1 To n
A(i, j) = ActiveCell
ActiveCell.Offset(0, 1).Range("A1").Select
Next j
ActiveCell.Offset(0, -n).Range("A1").Select
Next i
【手順1−1】非対角要素で絶対値最大なものをみつける
対象の行列が対称行列であるので、対角要素の右上か左下の何れかを調べればよいことになる。
ここでは、右上を調べることにする。調べるべき要素は次のようになる。
A(1, 2), A(1, 3), ... , A(1, n)
A(2, 3), ... , A(2, n)
:
A(n-1, n)
最大値をみつける手順は、“仮の最大数”を与えておいて、その値と上記のデータを順に比較し、
より大きい値がみつかったときに“仮の最大数”を置き換えればよいことになる。
abc:
z = -1
For i = 1 To n-1: For j = i+1 To n
If Abs(A(i, j)) > z Then z = Abs(A(i, j)): ii = i: jj = j
Next j: Next i
「For i = 1 To n-1: For j = i+1 To n」は多重文と呼ばれるもので、本来は2行に分けて記述
すべきところを1行にまとめて記述したもので、コロン(:)で区切って記述すればよいことにな
っている。「If Abs(A(i, j)) > z Then z = Abs(A(i, j)): ii = i: jj = j」は1行IF文であ
り、基本形は『If 条件文 Then 命令(多重文も可) Else 命令(多重文も可)』と1行で記述す
るもので、Else以下は省略可能であり、End Ifは記さない。命令の部分が短いとき利用すると便利
なものである。
ここでは、仮の最大数を保存する変数がzであり、当初 -1 としているのは、その値が絶対選ば
れないようにするためである。変数iiとjjには最大数のみつかった場所が保存される。Abs(・)は
絶対値を計算する関数である。abc: はラベルであり、全体の手順を繰り返すときに、戻る場所を
指示するためのものである。
【手順1−2】みつかった絶対値最大の値が微少のときは、繰り返し作業を終了する
If z < 1E-10 Then GoTo xyz
1E-10は1×10-10=0.0000000001であり、GoTo xyzはラベルxyz: にジャンプせよとの命令である。
【手順2】回転角の計算
t = Atn(2*A(ii, jj) / (A(ii, ii)-A(jj, jj))) / 2
Atn(・)はアークタンジェントを計算する関数である。ただし、A(ii, ii)-A(jj, jj)=0のときは
“0割り”となり、計算が停止する。そこで次のようにする。
If Abs(A(ii, ii)-A(jj, jj)) < 1E-10 Then
t = 3.14159265358979 / 4
Else
t = Atn(2*A(ii, jj) / (A(ii, ii)-A(jj, jj))) / 2
End If
すなわち、A(ii, ii)-A(jj, jj) が非常に0に近いときは、回転角tをπ/4にすることを意味し
ている。
【手順3】回転行列の作成
For i = 1 To n
For j = 1 To n: B(i, j) = 0: Next j
B(i, i) = 1
Next i
B(ii, ii) = Cos(t): B(jj, jj) = Cos(t)
B(ii, jj) = Sin(t): B(jj, ii) = -Sin(t)
【手順4】BABTの計算
三つの行列の積を計算しなければならないが、最初に BA を計算して C に保存し、次に CBT を
計算することにする。BA の計算は次のようになる。
For i = 1 To n: For j = 1 To n
S = 0
For k = 1 To n: S = S + B(i, k)*A(k, j): Next k
C(i, j) = S
Next j: Next i
For i = 1 To n: For j = 1 To n
S = 0
For k = 1 To n: S = S + C(i, k)*B(j, k): Next k
A(i, j) = S
Next j: Next i
GoTo abc
下から4行目で B(j, k) とあるが、これは BT を意味している。下から3行目で CBT=BABT をAに
保存しているが、これは次の繰り返し計算のためである。最後の行は、次の繰り返し計算へ進む命
令である。
上記のプログラムは、3つの行列の積BABTを求めるときに、まず2つの行列積BAをCとして求め、
次に行列積CBTを求めている。行列計算に慣れていないと理解しにくいかもしれないが、3つの行列
積を一度に計算することも可能であり、そのプログラムは次のようになる。
For i = 1 To n: For j = 1 To n
S = 0
For p = 1 To n: For q = 1 To n
S = S + B(i, p) * A(p, q) * B(j, q)
Next q, p
C(i, j) = S
Next j, i
For i = 1 To n: For j = 1 To n
A(i, j) = C(i, j)
Next j, i
GoTo abc
ここで注意すべきことは、前半の部分で計算結果をCに代入し、後半でCをAにコピーしていることで
ある。前半で、計算結果を直接Aに代入できないのは、Aを計算に用いている最中にAを変えると、計
算が無意味なものになってしまうからである。
【手順5】結果の出力
求める固有値は行列Aの対角要素であり、現在のアクティブセルは、最初の固有値を出力するセ
ルの2つ上であるので、プログラムは次のようになる。
xyz:
ActiveCell.Offset(2, 0).Range("A1").Select
For k = 1 To n
ActiveCell = A(k, k)
ActiveCell.Offset(0, 1).Range("A1").Select
Next k
先頭のxyz: はラベルであり、手順1−2からのジャンプ先である。
|
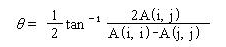 【手順3】
単位行列で、(i,i)要素と(j,j)要素をcosθ、(i,j)要素をsinθ、(j,i)要素を-sinθに置き換えた
回転行列Jを考える。回転行列JはJ-1=JTという性質を持っている。
【手順4】
相似変換JAJ-1=JAJTを求め、その結果を新たなAとして手順1へ戻る。
【手順5】
非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみなすこ
とができ、各対角要素が固有値となる。
【手順3】
単位行列で、(i,i)要素と(j,j)要素をcosθ、(i,j)要素をsinθ、(j,i)要素を-sinθに置き換えた
回転行列Jを考える。回転行列JはJ-1=JTという性質を持っている。
【手順4】
相似変換JAJ-1=JAJTを求め、その結果を新たなAとして手順1へ戻る。
【手順5】
非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみなすこ
とができ、各対角要素が固有値となる。
 非対角要素で絶対値最大なものはA(1, 2)=A(2, 1)=2 であるから、回転角θは
非対角要素で絶対値最大なものはA(1, 2)=A(2, 1)=2 であるから、回転角θは
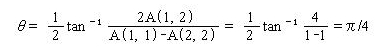
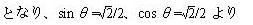
 相似変換は
相似変換は