実対称行列の固有ベクトル計算
ヤコビ法による固有値計算手順は
A1 = B1AB1-1
A2 = B2A1B2-1
A3 = B3A2B3-1
のようにして、非対角要素がほぼ0になるまで順次A1、A2、A3、・・・を求めるものである。m回の繰
り返しで、非対角要素がほぼ0になったとすると、Am は非対角要素が0であり、対角要素それぞれが
固有値を表す行列となる。また
Am = Bm ・・・ B2B1AB1-1B2-1 ・・・ Bm-1 = (Bm ・・・ B2B1)A(Bm ・・・ B2B1)-1
であるので
B = (Bm ・・・B2B1)-1 = B1-1B2-1・・・Bm-1 = B1TB2T ・・・ BmT = (Bm ・・・ B2B1)T
とすれば、Am=B-1AB、すなわち、BAm=AB となる。Am の第i対角要素をλi、B の第i列を bi とすれば
λibi = Abi
となり、bi は固有値 λi に対応した固有ベクトルとなる。
したがって、ヤコビ法の手順に赤字で示す操作を追加すれば、固有値と共に固有ベクトルも求められ
ることになる。
【手順0】
Bを単位行列とする。
【手順1】行列Aの非対角要素で絶対値が最大な要素を見つける。それがA(i, j)=A(j, i)であったもの
とし、その値が許容される値よりも小さいときは反復計算を終了し手順5へ進み、さもないときは
手順2へ進む。ただし、A(i, j)は行列Aの上からi行目、左からj列目の要素を意味する。許容され
る値としては、ほとんど0とみなすことができる値(例えば10-10)を設定する。
【手順2】回転角θを次式により求める。
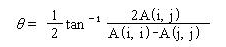 【手順3】単位行列で、(i, i)要素と(j, j)要素をcosθ、(i, j)要素をsinθ、(j, i)要素を-sinθに
置き換えた回転行列Jを考える。回転行列 J は J-1 = JT という性質を持っている。
【手順4】相似変換JAJ-1 = JAJT と BJT = BJ-1 を求め、その結果をそれぞれ新たなAとBとして手順1
へ戻る。
【手順5】非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみな
すことができ、各対角要素が固有値であり、Bの各列が固有ベクトルとなる。
【手順3】単位行列で、(i, i)要素と(j, j)要素をcosθ、(i, j)要素をsinθ、(j, i)要素を-sinθに
置き換えた回転行列Jを考える。回転行列 J は J-1 = JT という性質を持っている。
【手順4】相似変換JAJ-1 = JAJT と BJT = BJ-1 を求め、その結果をそれぞれ新たなAとBとして手順1
へ戻る。
【手順5】非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみな
すことができ、各対角要素が固有値であり、Bの各列が固有ベクトルとなる。
固有値および固有ベクトルを計算するためのEXCELマクロは次のようになる。赤字部分は、固有ベク
トルを計算するために固有値計算マクロに追加される部分である。ただし、上記説明でBとした行列は、
配列Wとしてあるので、注意して下さい。
n = ActiveCell
ReDim A(n, n), B(n, n), C(n, n), W(n, n), D(n, n)
ActiveCell.Offset(1, 0).Range("A1").Select
For i = 1 To n
For j = 1 To n
A(i, j) = ActiveCell
ActiveCell.Offset(0, 1).Range("A1").Select
Next j
ActiveCell.Offset(1, -n).Range("A1").Select
Next i
For i = 1 To n
For j = 1 To n
W(i, j) = 0
Next j
W(i, i) = 1
Next i
'
abc:
z = -1
For i = 1 To n - 1
For j = i + 1 To n
If Abs(A(i, j)) > z Then
z = Abs(A(i, j)): ii = i: jj = j
End If
Next j
Next i
If z < 0.0000000001 Then GoTo xyz
AA = A(ii, ii) - A(jj, jj)
If Abs(AA) < 0.0000000001 Then
t = 3.1415926538979 / 4
Else
t = Atn(2 * A(ii, jj) / AA) / 2
End If
For i = 1 To n
For j = 1 To n
B(i, j) = 0
Next j
B(i, i) = 1
Next i
B(ii, ii) = Cos(t): B(jj, jj) = Cos(t)
B(ii, jj) = Sin(t): B(jj, ii) = -Sin(t)
For i = 1 To n: For j = 1 To n
s = 0
For p = 1 To n: For q = 1 To n
s = s + B(i, p) * A(p, q) * B(j, q)
Next q, p
C(i, j) = s
Next j, i
For i = 1 To n: For j = 1 To n
s = 0
For p = 1 To n
s = s + W(i, p) * B(j, p)
Next p
D(i, j) = s
Next j, i
For i = 1 To n: For j = 1 To n
A(i, j) = C(i, j)
W(i, j) = D(i, j)
Next j, i
GoTo abc
xyz:
ActiveCell.Offset(1, 0).Range("A1").Select
For i = 1 To n
ActiveCell = A(i, i)
ActiveCell.Offset(0, 1).Range("A1").Select
Next i
ActiveCell.Offset(2, -n).Range("A1").Select
For i = 1 To n
For j = 1 To n
ActiveCell = W(i, j)
ActiveCell.Offset(0, 1).Range("A1").Select
Next j
ActiveCell.Offset(1, -n).Range("A1").Select
Next i
|
|
固有値・固有ベクトル計算マクロのSUBプロシージャ化
|
|---|
固有値・固有ベクトル計算部分
For i = 1 To n
For j = 1 To n: W(i, j) = 0: Next j
W(i, i) = 1
Next i
abc:
z = -1
For i = 1 To n-1: For j = i+1 To n
If Abs(A(i, j)) > z Then z = Abs(A(i, j)): ii = i: jj = j
Next j, i
If z < 1E-10 Then GoTo xyz
AA = A(ii, ii) - A(jj, jj)
If Abs(AA) < 1E-10 Then
t = 3.14159265358979 / 4
Else
t = Atn(2 * A(ii, jj) / AA) / 2
End If
For i = 1 To n
For j = 1 To n: B(i, j) = 0: Next j
B(i, i) = 1
Next i
B(ii, ii) = Cos(t): B(jj, jj) = Cos(t)
B(ii, jj) = Sin(t): B(jj, ii) = -Sin(t)
For i = 1 To n: For j = 1 To n
S = 0
For p = 1 To n: For q = 1 To n
S = S + B(i, p) * A(p, q) * B(j, q)
Next q, p
C(i, j) = S
Next j, i
For i = 1 To n: For j = 1 To n
s = 0
For p = 1 To n
s = s + W(i, p) * B(j, p)
Next p
D(i, j) = s
Next j, i
For i = 1 To n: For j = 1 To n
A(i, j) = C(i, j)
W(i, j) = D(i, j)
Next j, i
GoTo abc
xyz:
で、この部分だけで使用される変数は、z、i、j、ii、jj、t、B、S、p、q、C、Dであり、nとAは他の
部分で決められており、ここで計算されるAとWは他の部分で使用される。
したがって、引数をA、W、nにすればよいことになる。SUBプロシージャ名をeigenとしたとき、上の
プログラムをSUBプロシージャ化したものは次のようになる。
Sub eigen(A, W, n)
ReDim B(n, n), C(n, n), D(n, n)
For i = 1 To n
For j = 1 To n: W(i, j) = 0: Next j
W(i, i) = 1
Next i
abc:
z = -1
For i = 1 To n-1: For j = i+1 To n
If Abs(A(i, j)) > z Then z = Abs(A(i, j)): ii = i: jj = j
Next j, i
If z < 1E-10 Then Exit Sub
AA = A(ii, ii) - A(jj, jj)
If Abs(AA) < 1E-10 Then
t = 3.14159265358979 / 4
Else
t = Atn(2 * A(ii, jj) / AA) / 2
End If
For i = 1 To n
For j = 1 To n: B(i, j) = 0: Next j
B(i, i) = 1
Next i
B(ii, ii) = Cos(t): B(jj, jj) = Cos(t)
B(ii, jj) = Sin(t): B(jj, ii) = -Sin(t)
For i = 1 To n: For j = 1 To n
S = 0
For p = 1 To n: For q = 1 To n
S = S + B(i, p) * A(p, q) * B(j, q)
Next q, p
C(i, j) = S
Next j, i
For i = 1 To n: For j = 1 To n
s = 0
For p = 1 To n
s = s + W(i, p) * B(j, p)
Next p
D(i, j) = s
Next j, i
For i = 1 To n: For j = 1 To n
A(i, j) = C(i, j)
W(i, j) = D(i, j)
Next j, i
GoTo abc
End Sub
ここで注意すべきことは、赤字の部分である。
まず、配列B、C、DはこのSUBプロシージャでのみ使用され、他の部分で定義することができないの
でReDim B(n, n), C(n, n), D(n, n)と、定義しなければならない。ただし、引数であるAとWはこの
SUBプロシージャを呼び出す部分で定義してあるはずであるから、ここで定義する必要がない。
Exit Subは、SUBプロシージャを終了するための命令であり、End Subに達したときと同様に、呼び
出したところに処理を戻すことになる。
元々が GoTo xyz → xyz: → End Sub となるものであることから、GoTo xyz を Exit Sub に置き
換えてよく、ラベル xyz: が不要になったため省略してある。
さらに、青字にした部分を見比べると、配列がWとBで異なるのみで、同型であることに気付くであ
ろう。このように同型になっている部分は、SUBプロシージャ化すべき候補となる。
これらのプログラムは、配列WないしBを単位行列にするためのものであり、SUBプロシージャ化す
れば、次のようになる。
Sub S2(x, n)
For i = 1 To n
For j = 1 To n: x(i, j) = 0: Next j
x(i, i) = 1
Next i
End Sub
このSUBプロシージャS2を用いれば、先のSUBプロシージャeigenは次のようになる。
Sub eigen(A, W, n)
ReDim B(n, n), C(n, n), D(n, n)
Call S2(W, n)
abc:
z = -1
For i = 1 To n-1: For j = i+1 To n
If Abs(A(i, j)) > z Then z = Abs(A(i, j)): ii = i: jj = j
Next j, i
If z < 1E-10 Then Exit Sub
AA = A(ii, ii) - A(jj, jj)
If Abs(AA) < 1E-10 Then
t = 3.14159265358979 / 4
Else
t = Atn(2 * A(ii, jj) / AA) / 2
End If
Call S2(B, n)
B(ii, ii) = Cos(t): B(jj, jj) = Cos(t)
B(ii, jj) = Sin(t): B(jj, ii) = -Sin(t)
For i = 1 To n: For j = 1 To n
S = 0
For p = 1 To n: For q = 1 To n
S = S + B(i, p) * A(p, q) * B(j, q)
Next q, p
C(i, j) = S
Next j, i
For i = 1 To n: For j = 1 To n
s = 0
For p = 1 To n
s = s + W(i, p) * B(j, p)
Next p
D(i, j) = s
Next j, i
For i = 1 To n: For j = 1 To n
A(i, j) = C(i, j)
W(i, j) = D(i, j)
Next j, i
GoTo abc
End Sub
プログラムを、上記のSUBプロシージャを用いて書き直せば、次のようになる。
n = ActiveCell
ReDim A(n, n), W(n, n)
ActiveCell.Offset(1, 0).Range("A1").Select
For i = 1 To n
For j = 1 To n
A(i, j) = ActiveCell
ActiveCell.Offset(0, 1).Range("A1").Select
Next j
ActiveCell.Offset(1, -n).Range("A1").Select
Next i
'
Call eigen(A, W, n)
'
ActiveCell.Offset(1, 0).Range("A1").Select
For i = 1 To n
ActiveCell = A(i, i)
ActiveCell.Offset(0, 1).Range("A1").Select
Next i
ActiveCell.Offset(2, -n).Range("A1").Select
For i = 1 To n
For j = 1 To n
ActiveCell = W(i, j)
ActiveCell.Offset(0, 1).Range("A1").Select
Next j
ActiveCell.Offset(1, -n).Range("A1").Select
Next i
さらに、頻繁に出てくるアクティブセル移動命令
ActiveCell.Offset(*, *).Range("A1").Select
をSUBプロシージャ化する。SUBプロシージャ名をS1とすればSUBプロシージャは次にようになる。
Sub S1(x, y)
ActiveCell.Offset(x, y).Range("A1").Select
End Sub
このとき、本文での
ActiveCell.Offset(0, 1).Range("A1").Select
は
Call S1(0, 1)
と簡単化される。したがって、固有値計算マクロ本文は次のようになる。
n = ActiveCell
ReDim A(n, n), W(n, n)
Call S1(1, 0)
For i = 1 To n
For j = 1 To n
A(i, j) = ActiveCell: Call S1(0, 1)
Next j
Call S1(1, -n)
Next i
'
Call eigen(A, W, n)
'
Call S1(1, 0)
For i = 1 To n
ActiveCell = A(i, i): Call S1(0, 1)
Next i
Call S1(2, -n)
For i = 1 To n
For j = 1 To n
ActiveCell = W(i, j): Call S1(0, 1)
Next j
Call S1(1, -n)
Next i
|
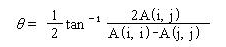 【手順3】単位行列で、(i, i)要素と(j, j)要素をcosθ、(i, j)要素をsinθ、(j, i)要素を-sinθに
置き換えた回転行列Jを考える。回転行列 J は J-1 = JT という性質を持っている。
【手順4】相似変換JAJ-1 = JAJT と BJT = BJ-1 を求め、その結果をそれぞれ新たなAとBとして手順1
へ戻る。
【手順5】非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみな
すことができ、各対角要素が固有値であり、Bの各列が固有ベクトルとなる。
【手順3】単位行列で、(i, i)要素と(j, j)要素をcosθ、(i, j)要素をsinθ、(j, i)要素を-sinθに
置き換えた回転行列Jを考える。回転行列 J は J-1 = JT という性質を持っている。
【手順4】相似変換JAJ-1 = JAJT と BJT = BJ-1 を求め、その結果をそれぞれ新たなAとBとして手順1
へ戻る。
【手順5】非対角要素で絶対値が最大なものの値が非常に小さいので、得られた行列は対角行列とみな
すことができ、各対角要素が固有値であり、Bの各列が固有ベクトルとなる。