3. MS-Excelによる回帰分析
3.1 回帰分析とは何か
回帰分析とは,何らかの変量(値が変動するもの)があるとき,その変動の原因を統計的に(データ
を基に)究明し,それらの関係を表す“回帰モデル”と呼ばれる数式を求めることである.回帰分析に
おいては,原因自身も何らかの変量であるものとしている.すなわち,原因となる量が変動するから結
果としての量も変動すると考えている.
まずすべきことは,原因が何であるかを決定することであるが,一般的には,分析者が主観的に決定
している.このとき,経済理論等に関する知識が,原因を決定する際の手助けとなるであろう.
変動の原因を究明したい変量をYで表すことにする.また,原因と考えられる変量がk個あり,それ
ぞれをX1,X2,・・・ ,Xkで表すことにする.このとき,これらの変量の関係を数式で表せば
Y=f(X1,X2,・・・ ,Xk)+u
となる.ここで,uはその影響が些細であると考えられたため無視された原因をまとめたものであり,
“撹乱項”と呼ばれる.また,X1,X2,・・・ ,Xk は“説明変数”,Yは“被説明変数”と呼ばれる.
この段階での数式 f(X1,X2,・・・ ,Xk) は一般形でありデータを用いた分析にはそぐわない.そこ
で,この数式を次のような回帰モデルとして具体化(“特定化”と呼ばれる)する.
Y=β0+β1X1+β2X2+・・・+βkXk+u
この回帰モデルを分析するためには,データが組(Y,X1,X2,・・・ ,Xk)として多数存在することが
必要である.ここでは,データがn組利用できるものとする.すなわち,
(Y1,X11,X21,・・・ ,Xk1)
(Y2,X12,X22,・・・ ,Xk2)
:
:
(Yn,X1n,X2n,・・・ ,Xkn)
のようにデータがあるものとする.
回帰分析とは,これらのデータを用いて回帰モデルの係数 β0,β1,β2,・・・,βk と,撹乱項uがどの
ようなものであるかを“推定”することである.ここで“推定”という言葉を用いたのは,現在のデー
タを用いて求められたこれらの値と,データが追加されたときに求められる値とは必ずしも一致せず,
どちらが正しいのか不明であり,あくまでも現在のデータを基にして正しいと思われる値が求められた
に過ぎないことから“推定”という言葉が用いられる.
n組のデータから k+1個の係数を推定することになるので,n>kでなければならないだけでなく,
できるだけその差が大きいことが望ましく,データ数nはkの約10倍以上であることが必要であろう.
このことからデータ数が少ないときは,説明変数の個数kに制約が設けられることになり,やみくもに
多くすることはできない.
3.2 回帰分析の方法
データを回帰モデルに代入すると
Y1 = β0 + β1X11 + β2X21 +・・・+ βkXk1 + u1
Y2 = β0 + β1X12 + β2X22 +・・・+ βkXk2 + u2
:
:
Yn = β0 + β1X1n + β2X2n +・・・+ βkXkn + un
のようにn本の連立方程式が得られる.ここで
┌ Y1 ┐ ┌ u1 ┐
│ Y2 │ │ u2 │
Y =│ : │, u =│ : │,
│ : │ │ : │
└ Yn ┘ └ un ┘
|
┌ 1 X11 X21 ・・・ Xk1 ┐
│ 1 X12 X22 ・・・ Xk2 │
X =│ : : : : │,
│ : : : : │
└ 1 X1n X2n ・・・ Xkn ┘
|
β =
|
┌ β0
│ β1
│ :
│ :
└ βk
|
┐
│
│
│
┘
|
とすると,上の連立方程式は次式のようにまとめて記述することができる.
Y=Xβ+u
回帰係数 β0,β1,・・・,βk の推定量をそれぞれ b0,b1,・・・,bk で表し,b = [b0 b1 ・・・ bk]T とす
る.ただし,上付きのTは転置を意味する.さらに,
Y^ = Xb, e = Y - Y^ = Y - Xb, e = [e1 e2 ・・・ en]T
とすれば,
Y = Xb + e
となり,eは“残差”と呼ばれる.元の回帰モデルと比較したとき,bがβに近ければ近いほど,eは
uに似たものとなりuの推定量とみなすこともできる.
ここでの分析の立場からすると,無視した原因を集計したものである撹乱項uは小さいことが望まし
い.同様に,残差eも小さいことが望ましい.真の係数ベクトルβが不明である限り撹乱項uも不明で
あるが,残差eは係数ベクトルβの推定量であるbが求められれば計算可能である.このことから,e
を最小にすることを考える.しかし,eはn次元ベクトルでありn個の要素からなるため,単純に大小
を比較する方法がない.そこで,ベクトルeの長さの2乗(長さの2乗が最小になれば長さも最小にな
る)をもって大小比較の基準とする.すなわち
eの長さの2乗 = eTe = e12 + e22 +・・・+ en2
であるので,残差平方和を最小にするようなbを求めることを考える.
eTe = (Y-Xb)T(Y-Xb) = YTY - 2YTXb + bTXTXb
をbで偏微分すれば,∂eTe/∂b = -2XTY + 2XTXb,∂2eTe/∂b2=2XTX>0となるので -2XTY + 2XTXb = 0
の解
b = (XTX)-1XTY
は残差平方和 eTe を最小にする.このようにしてbを求める方法は“最小2乗法”と呼ばれる.
ここでは,係数ベクトルβの推定量として,最小2乗法によって求められるbを考えているが,これ
でよいのであろうか,これ以外にもっと良い推定量があるのではないかという疑問が生じる.実は,最
も良い推定量を得るための方法として“最尤法”と呼ばれる方法が存在する.しかし,最尤法は難しい
方法であるため,一般には用いられず,最小2乗法の結果と最尤法の結果との差が理論的に検討されて
いる.
この理論的検討を可能とするために,攪乱項 u1,u2,・・・,un が確率変数であると仮定する.すなわ
ち,u1,u2,・・・,un は,それぞれがある確率分布を持った母集団 U1, U2,・・・, Un からの標本(サン
プル)であると考える.この仮定は,仮に説明変数(X1i, X2i,・・・, Xki)が同じ値になったとしても,
無視した原因を集計した ui の値が異なるため,Yi が異なる値になることを意味し,直感と矛盾しない
仮定であろう.
攪乱項を確率変数と仮定すると,被説明変数 Y1, Y2,・・・, Yn も確率変数となり,確率変数 Y1,Y2,
・・・, Yn を用いて求められるbは統計量(確率変数を含む計算式)となる.その意味するところは,現
在n組のデータがあるが,再度同じ説明変数の値の下でデータを取り直してみたとき(現実には実現不
可能なことの多い架空の想定),攪乱項が異なる値になるため Y1, Y2,・・・, Yn も異なる値になり,b
も大きくは違わないにしても異なる値になり,結果的にbは確率分布するであろうというものである.
まず,次の仮定を置く.
Ⅰ 各母集団 U1, U2,・・・, Un の平均値は0である.したがって,E(ui) = 0,i=1,2,・・・,n.
Ⅱ 各母集団 U1, U2,・・・, Un の分散は均一である.したがって,E(ui2) = σ2,i=1,2,・・・,n.
Ⅲ 各母集団 U1, U2,・・・, Un からの標本抽出(攪乱項の出現)が独立である.
したがって,E(uiuj) = 0,i≠j;i,j=1,2,・・・,n.
これらの仮定が成り立つとき,最小2乗推定量bはβの最良線形不偏推定量(Best Linear Unbiased
Estimator,略してBLUEと呼ぶ)となる.すなわち,最小2乗推定量bは不偏性(E(b)=β)を満たすす
べての線形推定量(b = CYとなる推定量)の中で,分散が最小な推定量となる.さらに,次の仮定を
追加する.
Ⅳ 各母集団U1, U2,・・・, Unは正規分布する.したがって,上の仮定と合わせると,攪乱項ベクトル
uは多変量正規分布 N(0, σ2I) に従うことになる.
以上4つの仮定が成り立つとき,最小2乗推定量bは最尤法によって求められる推定量に一致する.
すなわち,この4つの仮定が成り立つならば,最小2乗推定量bは最も良い推定量ということになる.
逆にこれらの仮定の内1つでも成り立たないとすれば,最小2乗推定量bは最も良いという保証がな
く,もっと良い推定量の存在を否定できないため,使用できないことになる.
これまでに述べた4つの仮定以外にも,回帰分析において前提とされる次の仮定がある.
Ⅴ n組のデータが構造的に差のない対象から得られたものであること.
Ⅵ 説明変数 X1, X2,・・・, Xk が非確率変数であること.
Ⅶ 説明変数行列Xの階数(ランク)が k+1,言い換えれば XTX が正則であること.
Excelによる回帰分析の手順
次表のデータを基にしてExcelによる回帰分析の手順を説明する.
ここでは,原油輸入量の変動をその他の変量を用いて説明するモデル
Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + β5X5 + u
を考える.ただし,Y:原油輸入量,X1:原油輸入価格,X2:鉱工業生産指数,X3:卸売物価指数,
X4:石炭消費量,X5:石炭輸入価格である.
| | 原油 | 鉱工業
生産指数 | 卸売
物価指数 | 石炭 |
| |
輸入量 | 輸入価格 |
消費量 | 輸入価格 |
| | 100万kl |
1000円/kl | 1975=100 |
1975=100 | 100万t |
1000円/t |
| 1967 |
120.6 | 4.34 |
60.5 | 59.7 |
78.5 | 5.67 |
| 1968 |
139.8 | 4.34 |
69.7 | 60.3 |
83.4 | 5.76 |
| 1969 |
167.4 | 4.10 |
80.7 | 61.5 |
87.7 | 5.90 |
| 1970 |
197.1 | 4.08 |
91.8 | 63.8 |
89.3 | 7.20 |
| 1971 |
222.3 | 4.80 |
94.3 | 63.3 |
80.5 | 7.49 |
| 1972 |
249.2 | 4.85 |
101.1 | 63.8 |
75.9 | 6.75 |
| 1973 |
289.7 | 5.61 |
116.2 | 73.9 |
81.2 | 6.47 |
| 1974 |
278.4 | 19.75 |
111.7 | 97.1 |
86.2 | 12.72 |
| 1975 |
263.4 | 22.12 |
100.0 | 100.0 |
81.8 | 16.57 |
| 1976 |
267.8 | 23.50 |
111.0 | 105.0 |
78.6 | 17.40 |
| 1977 |
278.0 | 22.92 |
115.6 | 107.0 |
78.4 | 15.76 |
| 1978 |
270.7 | 18.37 |
122.7 | 104.3 |
69.4 | 12.49 |
| 1979 |
281.2 | 26.12 |
132.8 | 111.9 |
75.7 | 13.18 |
| 1980 |
254.4 | 47.19 |
141.8 | 131.8 |
87.8 | 14.82 |
| 1981 |
227.4 | 51.55 |
146.2 | 134.1 |
95.9 | 15.53 |
手順1: 図1のようにExcelのワークシートにデータを入力する.
ここで注意すべきことは,データを縦に並べることと,説明変数のデータを連続した列に長方形に
並べることである.なお,被説明変数と説明変数は離れていてもかまわない.
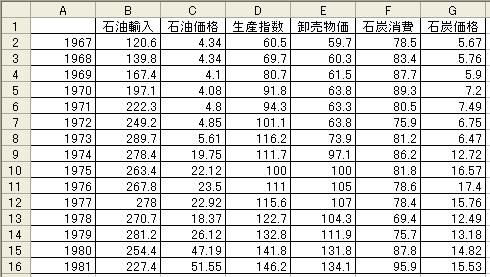 図1
手順2:メニューバーの【ツール(T)】をクリックし,開かれたメニューの【分析ツール(D)】をクリッ
クする.すると,図2の「データ分析ウイザード」が開くので,図2のように【回帰分析】を選択
し“OK”ボタンをクリックする.
図1
手順2:メニューバーの【ツール(T)】をクリックし,開かれたメニューの【分析ツール(D)】をクリッ
クする.すると,図2の「データ分析ウイザード」が開くので,図2のように【回帰分析】を選択
し“OK”ボタンをクリックする.
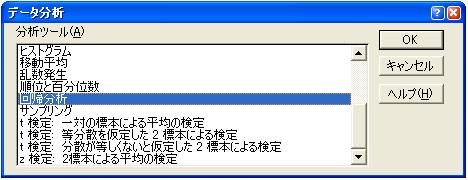 図2
手順3: 図3の「回帰分析ウイザード」が開くので,Y範囲として被説明変数のデータ範囲B2:B16を
指定する.さらに,X範囲として説明変数のデータ範囲C2:G16を指定する.その他にも色々な設定
が可能であるが,普通は,そのままOKボタンをクリックする.
図2
手順3: 図3の「回帰分析ウイザード」が開くので,Y範囲として被説明変数のデータ範囲B2:B16を
指定する.さらに,X範囲として説明変数のデータ範囲C2:G16を指定する.その他にも色々な設定
が可能であるが,普通は,そのままOKボタンをクリックする.
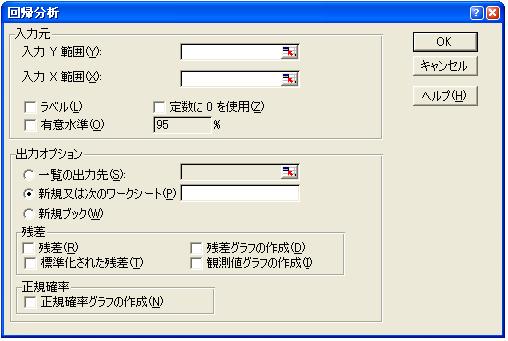 図3
範囲指定の具体的手順として,このウイザードが開いたとき,いわゆる“ペン”がY範囲指定欄に
あるので,データ範囲B2:B16をドラッグするか,セルB2をクリック(別のセルをクリックしてから
カーソル移動キーでB2まで移動してもよい)してからShiftキーを押しながらカーソル移動キーを
押して範囲を指定する.次にX範囲を指定するために,X範囲指定欄をクリックし、“ペン”をX
範囲指定欄に移動する.そして,Y範囲の場合と同様にして,説明変数のデータ範囲を指定する.
データ範囲を指定すると図4のようになるので,“OK”ボタンをクリックする.
図3
範囲指定の具体的手順として,このウイザードが開いたとき,いわゆる“ペン”がY範囲指定欄に
あるので,データ範囲B2:B16をドラッグするか,セルB2をクリック(別のセルをクリックしてから
カーソル移動キーでB2まで移動してもよい)してからShiftキーを押しながらカーソル移動キーを
押して範囲を指定する.次にX範囲を指定するために,X範囲指定欄をクリックし、“ペン”をX
範囲指定欄に移動する.そして,Y範囲の場合と同様にして,説明変数のデータ範囲を指定する.
データ範囲を指定すると図4のようになるので,“OK”ボタンをクリックする.
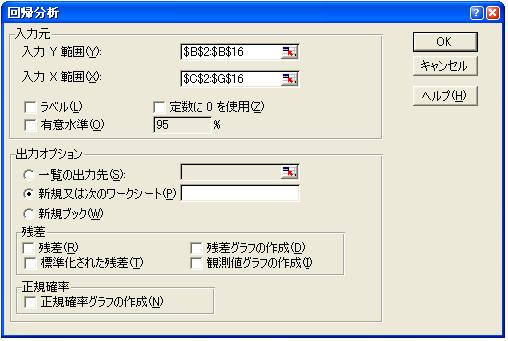 図4
以上の手順で回帰分析が実行され,結果が図5のように表示される.ただし,この計算結果は“新
しいワークシート”に表示される.係数の推定値 b0,b1,・・・,b5 は,それぞれB17からB22に表示
される.
図4
以上の手順で回帰分析が実行され,結果が図5のように表示される.ただし,この計算結果は“新
しいワークシート”に表示される.係数の推定値 b0,b1,・・・,b5 は,それぞれB17からB22に表示
される.
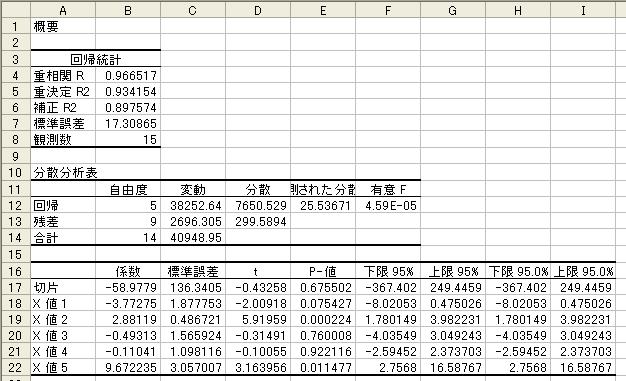 図5.回帰分析結果
3.3 回帰分析結果の評価
最小2乗法を用いれば,推定量bは必ず計算可能である.しかし,計算された推定量が信用に足るも
のであるかどうかの検定(テスト)が不可欠である.以下,最低限チェックすべき項目について説明す
る.
3.3.1 決定係数
最初に述べたように,回帰モデル
Y = β0 + β1X1 + β2X2 +・・・+ βkXk + u
は分析者が主観的に作成したものであり,本当にこのモデルで被説明変数Yの変動を説明できたのかど
うかを検定しなければならない.この検定のために用いられるのが“決定係数”である.
Y1, Y2,・・・, Yn の平均値を Y#,Xi1, Xi2,・・・, Xin の平均値を Xi#
yj = Yj-Y#, xij=Xij-Xi#, j=1,2,・・・,n;i=1,2,・・・,k
y^j = b0 + b1x1j + b2x2j +・・・+ bkxkj, j=1,2,・・・,n
とする.このとき,y=[y1 y2 ・・・ yn]T,y^=[y^1 y^2 ・・・ y^n]T とすれば
yTy = y^Ty^ + eTe
が成り立つ.ここで,左辺はYの平均値からの偏差の平方和であり,被説明変数Yの変動量と考えるこ
とができ,右辺第1項はここでのモデルで説明できた部分であり,第2項は説明できなかった不明な部
分とみなせる.したがって
R2 = y^Ty^/yTy
なる量を考えると,この値は全変動量中ここでのモデルで説明の付いた部分の割合となる.このことか
ら,この量は“決定係数”と呼ばれ,ここでのモデルのデータとの適合度のよさを測る尺度とされる.
決定係数 R2 が1であれば完全に説明が付いたことになるが,そのようなことは起こり得ず,普通は
0と1の間の値になる.それでは,決定係数 R2 はどのくらいであれば良いのかということになるが絶
対的な基準はない.おおよその目安として 0.6以上(説明の付かなかった部分の割合が 0.4以下)であ
ろう.
決定係数 R2 は,説明変数を追加(kが増加)すれば一般に増加する.決定係数に注目するあまり,
説明変数が多くなり過ぎると,モデルが複雑になるので,kが増加すればペナルティを受けるように修
正した決定係数が一般に利用される.それは
図5.回帰分析結果
3.3 回帰分析結果の評価
最小2乗法を用いれば,推定量bは必ず計算可能である.しかし,計算された推定量が信用に足るも
のであるかどうかの検定(テスト)が不可欠である.以下,最低限チェックすべき項目について説明す
る.
3.3.1 決定係数
最初に述べたように,回帰モデル
Y = β0 + β1X1 + β2X2 +・・・+ βkXk + u
は分析者が主観的に作成したものであり,本当にこのモデルで被説明変数Yの変動を説明できたのかど
うかを検定しなければならない.この検定のために用いられるのが“決定係数”である.
Y1, Y2,・・・, Yn の平均値を Y#,Xi1, Xi2,・・・, Xin の平均値を Xi#
yj = Yj-Y#, xij=Xij-Xi#, j=1,2,・・・,n;i=1,2,・・・,k
y^j = b0 + b1x1j + b2x2j +・・・+ bkxkj, j=1,2,・・・,n
とする.このとき,y=[y1 y2 ・・・ yn]T,y^=[y^1 y^2 ・・・ y^n]T とすれば
yTy = y^Ty^ + eTe
が成り立つ.ここで,左辺はYの平均値からの偏差の平方和であり,被説明変数Yの変動量と考えるこ
とができ,右辺第1項はここでのモデルで説明できた部分であり,第2項は説明できなかった不明な部
分とみなせる.したがって
R2 = y^Ty^/yTy
なる量を考えると,この値は全変動量中ここでのモデルで説明の付いた部分の割合となる.このことか
ら,この量は“決定係数”と呼ばれ,ここでのモデルのデータとの適合度のよさを測る尺度とされる.
決定係数 R2 が1であれば完全に説明が付いたことになるが,そのようなことは起こり得ず,普通は
0と1の間の値になる.それでは,決定係数 R2 はどのくらいであれば良いのかということになるが絶
対的な基準はない.おおよその目安として 0.6以上(説明の付かなかった部分の割合が 0.4以下)であ
ろう.
決定係数 R2 は,説明変数を追加(kが増加)すれば一般に増加する.決定係数に注目するあまり,
説明変数が多くなり過ぎると,モデルが複雑になるので,kが増加すればペナルティを受けるように修
正した決定係数が一般に利用される.それは
R^2 = 1-(1-R2)
|
n-1
―――
n-k-1
|
で計算されるものであり,“自由度修正済み決定係数”と呼ばれる.
Excelでの決定係数
Excelの回帰分析結果図5において,決定係数等は“回帰統計”欄に表示される.決定係数 R2 は
“重決定 R2”としてセルB5に表示され,自由度修正済み決定係数 R^2 は“補正 R2”としてセルB6に
表示される.なお,“重相関 R”としてセルB4に表示されるのは,決定係数の平方根であり,“標準誤
差”としてセルB7に表示されるのは,残差の標本標準偏差すなわち残差の標本分散(残差の平方和を残
差の自由度で割ったもの)の平方根である.データ数nはセルB8,残差の自由度(n-k)はセルB13に表
示される.ここでの例題の場合,自由度修正済み決定係数は89.8%であり,回帰モデルのデータとの適
合性に問題はないと考えられる.
3.3.2 t値
モデル全体の適合度の善し悪しは決定係数で検定するが,モデルに組み入れられた個々の説明変数が
本当に原因であったのかどうかを検定する必要がある.このために用いられるのが“t値”と呼ばれる
ものである.もしも,ある説明変数の係数 βi が0であったとすれば,その変量がどのように変動し
たとしてもYに対して影響を与えないことになる.すなわち,その説明変数はYの変動に対する原因で
ないということになり,回帰モデルから排除しなければならない.
前節で述べた仮定が成り立つとき,bは分布し,多変量正規分布 N(β,σ2(XTX)-1) に従い(ただし,
σ2 は撹乱項uの均一な分散である),行列 (XTX)-1 の第(i, i)要素を aii2 で表したとき,bi は正
規分布 N(βi,σ2aii2) に従うことになる.したがって,95%の確率で
βi-1.96σaii≦bi≦βi+1.96σaii
となる.この不等式を解き直せば,
bi-1.96σaii≦βi≦bi+1.96σaii
となる確率も95%となる.
0<bi - 1.96σaii≦βi≦bi + 1.96σaii
または
bi - 1.96σaii≦βi≦bi + 1.96σaii<0
すなわち
1.96<|bi/(σaii)|
であれば,信頼水準95%(有意水準5%)で βi = 0 となる可能性を否定することができる.
しかし,撹乱項uの分散 σ2 は未知であるので,計算可能な残差eの不偏分散 s2=eTe/(n-k-1) で推
定することにする(sはモデルの“標準誤差”と呼ばれる).このとき,(bi-βi)/(saii) は自由度
n-k-1 のt分布に従い,自由度 n-k-1 のt分布の有意水準5%(信頼水準95%)の棄却域の値を t0.05
で表せば,95%の確率で -t0.05≦(bi-βi)/(saii)≦t0.05 となる.したがって,t0.05<|bi/(saii)| であ
れば,信頼水準95%(有意水準5%)で βi=0 となる可能性を否定することができる.
saii は bi の“標準誤差”と呼ばれ,bi/(saii) は bi の“t値”と呼ばれる.t0.05 はt分布表と呼
ばれる数表から読み取らなければならないが,自由度が20のとき 2.086,30のとき 2.042,60のとき
2.000 であるので,普通は2が用いられる.すなわち,t値 bi/(saii) の絶対値が2以上のとき,Xi
は原因とみなしてよく,2以下のときは原因でないという疑いがはらせないことになる.t値の基準2
は厳しいので,基準として 21/2 = 1.4 を使うべきとの意見もある.
Excelでのt値
Excelの回帰分析結果図5において,各推定値のt値はD17からD22に表示される.また,E17からE22
にP-値,F17とG17からF22とG22に各係数の95%信頼区間の下限と上限が求められている.P-値とは,そ
れぞれの係数が0であるという帰無仮説を棄却し,係数が0でないすなわちその係数のかかっている変
数が原因であるという仮説を採択したとき,その判断が誤りである確率(第1種の過誤)を意味する.
95%信頼区間とは,推定しようとしている係数が95%の確率で存在する範囲を意味する.
ここでの例題では,説明変数 X4 の係数 β4 の推定値 b4 のt値が -0.101であり,そのP-値が92.2%
であるので,まず間違いなく説明変数 X4(石炭消費量)は原油輸入量の原因変数でないと考えられる.
したがって,説明変数 X4(石炭消費量)はモデルから排除されるべきである.その他にもt値が小さい
(すなわちP-値が大きい)ものがあるが,モデルから変数を排除するときは1つずつ行うのが一般的で
ある.石炭消費量を原因変数から排除したモデル
Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + u
を考える.ただし,Y:原油輸入量,X1:原油輸入価格,X2:鉱工業生産指数,X3:卸売物価指数,X4
:石炭輸入価格となる.このモデルの回帰分析をExcelで行うためには,図1のF列にある石炭消費量
データを削除しなければならないが,ここでは,図6のように石炭消費量以外のデータを別の場所にコ
ピーする方法を用いる.すなわち,①A1からG16を範囲指定し,Ctrlキーを押しながらキー“C”を押
す.②セルA18をクリックしてからCtrlキーを押しながらキー“V”を押す.③削除すべきF18からF33
を範囲指定し,Ctrlキーを押しながらキー“-”を押すと,“セルの削除ウイザード”が開くので,
“左方向にシフト”を選択して“OK”ボタンをクリックする.
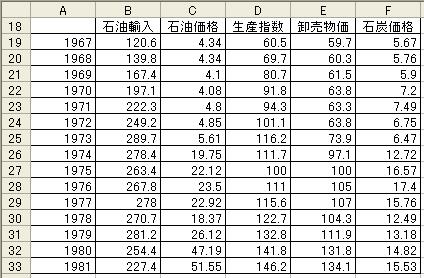 図6
ここで,Y範囲をB19:B33,X範囲をC19:F33として再度回帰分析を実施した結果の一部が図7であ
る.ここでのモデルでの説明変数 X3 の係数の推定値 b3 のt値が -0.329 であり,そのP-値が74.9%
であるので,説明変数 X3(卸売物価指数)も原油輸入量の原因変数でないと考えられる.したがっ
て,説明変数 X3(卸売物価指数)もモデルから排除されるべきである.
図6
ここで,Y範囲をB19:B33,X範囲をC19:F33として再度回帰分析を実施した結果の一部が図7であ
る.ここでのモデルでの説明変数 X3 の係数の推定値 b3 のt値が -0.329 であり,そのP-値が74.9%
であるので,説明変数 X3(卸売物価指数)も原油輸入量の原因変数でないと考えられる.したがっ
て,説明変数 X3(卸売物価指数)もモデルから排除されるべきである.
 図7
さらに卸売物価指数を原因変数から排除したモデル
Y = β0 + β1X1 + β2X2 + β3X3 + u
を考える.ただし,Y:原油輸入量,X1:原油輸入価格,X2:鉱工業生産指数,X3:石炭輸入価格とな
る.このモデルの回帰分析をExcelで行うために,図6のE列にある卸売物価指数データを削除した図
8のようなデータ領域を作成する.さらに,Y範囲をB36:B50,X範囲をC36:E50として再度回帰分析を
実施した結果が図9である.この結果において,すべての推定値のt値およびP-値は満足すべきもので
ある.
図7
さらに卸売物価指数を原因変数から排除したモデル
Y = β0 + β1X1 + β2X2 + β3X3 + u
を考える.ただし,Y:原油輸入量,X1:原油輸入価格,X2:鉱工業生産指数,X3:石炭輸入価格とな
る.このモデルの回帰分析をExcelで行うために,図6のE列にある卸売物価指数データを削除した図
8のようなデータ領域を作成する.さらに,Y範囲をB36:B50,X範囲をC36:E50として再度回帰分析を
実施した結果が図9である.この結果において,すべての推定値のt値およびP-値は満足すべきもので
ある.
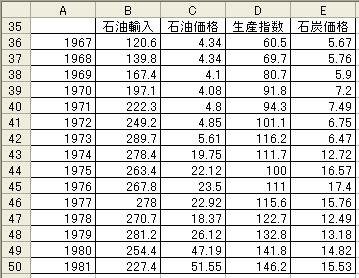 図8
図8
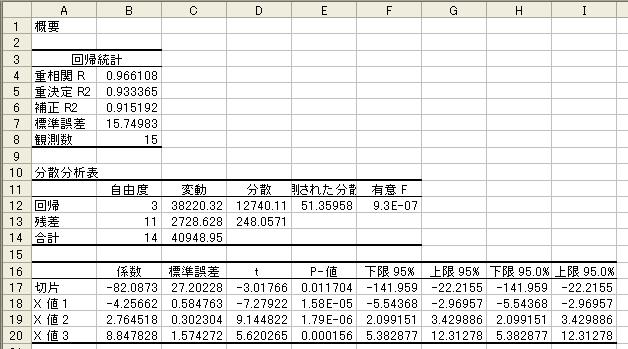 図9
3.3.3 撹乱項の独立性の検定
3.2節で述べた仮定Ⅲ(攪乱項の独立性)が成り立っているかどうかを検定する.この仮定は,時系
列データを扱う場合に成り立たなくことがある.時系列データ以外の場合は,一般にこの仮定は成り立
つと考えられ検定しないので,扱うデータが時系列データである場合の検定方法を以下で説明する.
攪乱項の独立性が損なわれるとき,最もよく起こることは,攪乱項の系列相関である.攪乱項の系列
相関とは,一度“+”の値になるとしばらく“+”の値が続き,“-”の値になると“-”の値が続く傾
向が見られることである.特に,前期と今期すなわち隣同士の間にこのような傾向(一階の自己相関と
呼ばれる)が見られるかどうかを検定する.一般に,一階の自己相関がないとき,攪乱項に自己相関が
ないすなわち攪乱項は独立であると判断される.
一階の自己相関があるとき,今期の攪乱項 uj と前期の攪乱項 uj-1 との間に uj=ρuj-1+εj という関
係が成り立つことになる.この関係が成り立つがどうかを検定する方法として,“ダービン・ワトソン
比”(“DW比”と略されることが多い)ないし“ダービンのh統計量”が用いられる.これらは状況に
よって使い分けられ,説明変数の中にラグ付き被説明変数(被説明変数を Yj としたとき Yj-1)が含ま
れないときはDW比を用い,含まれるときはダービンのh統計量を用いる.
DW比dは
図9
3.3.3 撹乱項の独立性の検定
3.2節で述べた仮定Ⅲ(攪乱項の独立性)が成り立っているかどうかを検定する.この仮定は,時系
列データを扱う場合に成り立たなくことがある.時系列データ以外の場合は,一般にこの仮定は成り立
つと考えられ検定しないので,扱うデータが時系列データである場合の検定方法を以下で説明する.
攪乱項の独立性が損なわれるとき,最もよく起こることは,攪乱項の系列相関である.攪乱項の系列
相関とは,一度“+”の値になるとしばらく“+”の値が続き,“-”の値になると“-”の値が続く傾
向が見られることである.特に,前期と今期すなわち隣同士の間にこのような傾向(一階の自己相関と
呼ばれる)が見られるかどうかを検定する.一般に,一階の自己相関がないとき,攪乱項に自己相関が
ないすなわち攪乱項は独立であると判断される.
一階の自己相関があるとき,今期の攪乱項 uj と前期の攪乱項 uj-1 との間に uj=ρuj-1+εj という関
係が成り立つことになる.この関係が成り立つがどうかを検定する方法として,“ダービン・ワトソン
比”(“DW比”と略されることが多い)ないし“ダービンのh統計量”が用いられる.これらは状況に
よって使い分けられ,説明変数の中にラグ付き被説明変数(被説明変数を Yj としたとき Yj-1)が含ま
れないときはDW比を用い,含まれるときはダービンのh統計量を用いる.
DW比dは
d =
|
n
Σ
j=2
|
(ej-ej-1)2 /
|
n
Σ
j=1
|
ej2
|
で計算される値であり,ダービンのh統計量は
h = (1-0.5d){n/(1-nv)}1/2
である.ただし,v は Yj-1 の係数の分散の推定量(先に述べた標準誤差の2乗)である.
DW比dの判定は,ダービンとワトソンが計算した表から,データ数nと説明変数の個数kを与えて
読みとられる2つの数値 dL と dU を用いて次のようになされる.
d<dL のとき,正の自己相関がある.
dU<d<4-dU のとき,自己相関がないという仮説が棄却できない.
4-dL<d のとき,負の自己相関がある.
dL<d<dU または 4-dU<d<4-dL のとき,結論が出せない.
ダービンのh統計量は近似的に標準正規分布 N(0, 1) に従うので,有意水準を10%とすれば
h<-1.645 のとき,負の自己相関がある.
-1.645<h<1.645 のとき,自己相関がないという仮説が棄却できない.
1.645<h のとき,正の自己相関がある.
なお,1-nv≦0 のときは,ダービンのh統計量が計算できないので,ej を ej-1 と元の回帰モデルに含
まれる説明変数とに回帰し,ej-1 との係数の有意性(t検定)で判定する.
ExcelでのDW比
Excelの回帰分析結果において,DW比は計算されないの
で,分析者が計算しなければならない.DW比を計算するた
めには残差を求めなければならないが,図4の“回帰分析ウ
イザード”において下から4行目左側の“残差(R)”をク
リックしてから“OK”ボタンをクリックすれば,図10のよう
に残差も計算される.ちなみに,残差と同時にB列に計算さ
れるのは Y^ である.
DW比を求めるために便利なExcel関数として,SUMSQ と
SUMXMY2(XマイナスYの2乗和)とがある.SUMSQ 関数は,
指定した範囲内のデータの2乗の和を計算し,SUMXMY2 関数
は指定した2つの範囲の対応するデータの差の2乗の和を計
算するものである.したがって,DW比の分子を計算するた
めに SUMXMY2 関数を用い,分母を計算するために SUMSQ 関
数を用いればよい.すなわち,適当なセルに
=SUMXMY2(C28:C41,C27:C40)/SUMSQ(C27:C41)
という数式を入力すればよい.このとき,DW比は 1.253
と計算される.
この値は系列相関があるかどうか判定不能であるため,ej
を ej-1 と元の回帰モデルに含まれる説明変数とに回帰し,
|
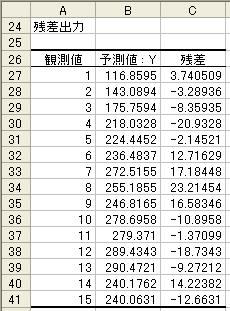 図10
図10
|
xej-1 との係数の有意性(t検定)で判定することにする.すなわち,回帰モデル
ej = β0 + β1X1 + β2X2 + β3X3 + β4ej-1 + u
を分析する.そのために図10のC26からC41を範囲指定し,Ctrl+C(Ctrlキーを押しながらキー“C”)
を押す.さらに,図8のデータが表示されるワークシートのセルF36をクリックしてからCtrl+V(Ctrl
キーを押しながらキー“V”)を押し,セルG35をクリックしてからCtrl+Vを押す.すると,図11のよう
になる.ここで,G列がejであり,F列がej-1に相当する.Y範囲をG37:G50とし,X範囲をC37:F50として
回帰分析を実施した結果から,ej-1の係数の推定値のt値は1.279であり,P-値は23.3%であるので,判定
は難しいが有意水準23.3%で系列相関があると判定できるであろう.
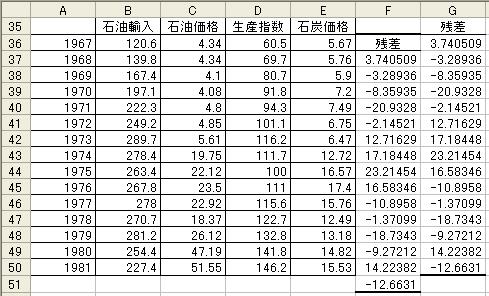 図11
3.3.4 自己相関がある(撹乱項が独立でない)場合の対処法
ここでは、コクラン・オーカット法と呼ばれる方法について説明する.
【手順1】: 本来の回帰モデルに対して最小2乗法を適用し,残差 e1,e2,・・・,en を求める.
図11
3.3.4 自己相関がある(撹乱項が独立でない)場合の対処法
ここでは、コクラン・オーカット法と呼ばれる方法について説明する.
【手順1】: 本来の回帰モデルに対して最小2乗法を適用し,残差 e1,e2,・・・,en を求める.
【手順2】: ρの推定値 r =
|
n
Σ
j=2
|
ejej-1 /
|
n
∑
j=2
|
ej-12 を求める.
|
【手順3】: Yj* = Yj-rYj-1,Xij* = Xij-rXij-1 (j=2,3,・・・,n;i=1,2,・・・,k)と変換し,変換された
データを用いて回帰分析を実施する.ただし,変換されたデータの個数は,元々のデータ個数よ
りも1つ少なくなることに注意すべきであろう.
Excelでの自己相関の対処法
手順2の推定値rを求めるとき,分母は先に説明したように SUMSQ 関数が便利であり,分子の計算の
ためには SUMPRODUCT 関数が便利である.SUMPRODUCT 関数は指定した2つの範囲の対応するデータの積
の和を計算するものである.図11が表示されるワークシートの適当なセル(ここではB52とする)に,
=SUMPRODUCT(G37:G50,G36:G49)/SUMSQ(G37:G49)
を入力する.すると,r=0.364827となる.
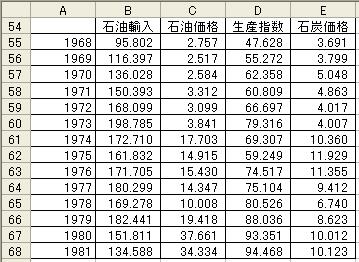 図12
このrを用いて手順3のデータを求めたものが図12である.ここで,セルB55に入力した数式は
=B37-$B$52*B36 であり,この数式をE68までコピーすることで図12が作成されている.Y範囲を
B55:B68とし,X範囲をC55:E68として回帰分析した結果が図13である.
図12
このrを用いて手順3のデータを求めたものが図12である.ここで,セルB55に入力した数式は
=B37-$B$52*B36 であり,この数式をE68までコピーすることで図12が作成されている.Y範囲を
B55:B68とし,X範囲をC55:E68として回帰分析した結果が図13である.
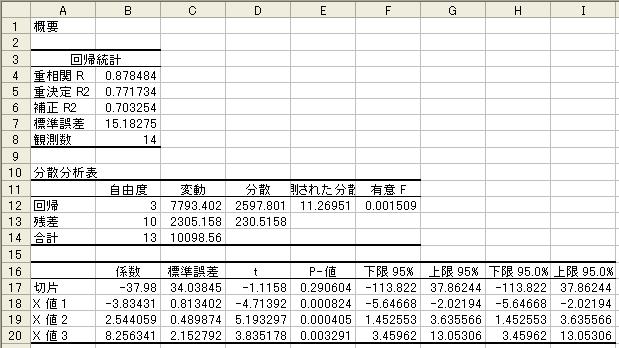 図13
3.3.5 分散均一性の検定
経済・経営分野での例においては,分散の不均一性が現れる場合,たいていは分散がいずれかの説明
変数と関連をもったものとなる.そのため,分散均一性の検定方法として,説明変数を用いたものが提
案されている.ここでは,数多くある検定方法の中で,最も機械的に処理可能な方法であるゴールドフ
ェルド・クォントの方法を説明する.
【手順1】撹乱項の分散と関係があると思われる説明変数の大きさの順にデータを並べ替える.
【手順2】並べ替えたデータのちょうど中間にあるc個のデータを省く.ただし,cはデータ総数n
の1/5から1/3の範囲で残りのデータ数が偶数となるように選ばれる.
【手順3】取り除かれた残りのデータの前半の(並べ替えのキーとなった説明変数が小さい値をもつ)
データ部分と後半の(説明変数が大きい値をもつ)データ部分それぞれに回帰分析を行う.
【手順4】各回帰分析結果の残差2乗和 ESS1(前半のデータに対応した残差2乗和)と ESS2(後半の
データに対応した残差2乗和)を求める.
【手順5】撹乱項が正規分布に従い,系列相関が存在しないとき,ESS2/ESS1 は自由度 (n-c-4)/2,
(n-c-4)/2 のF分布に従う.もし計算された ESS2/ESS1 がF分布の臨界値よりも小さいときは,
選択された有意水準で帰無仮説(分散均一の仮説)が採択され,大きいときは帰無仮説が棄却さ
れ対立仮説(分散不均一の仮説)が採択される.
3.3.6 分散が不均一である場合の対処法
【手順1】本来の回帰モデルに対して最小2乗法を適用し,残差 e1,e2,・・・,en を求める.
【手順2】撹乱項の分散のおおざっぱな推定値である残差の2乗データej2と,撹乱項の分散と関係が
あると思われる説明変数データ Xij とをプロットし,両者間の関係式を推定する.関係式とし
ては,
ej2 = cXij, ej2 = cXij2, ej2 = c/Xij
などが考えられる.
【手順3】上の推定された関係式に応じて,本来の回帰モデルの両辺を,Xi1/2,Xi,Xi-1/2 で割ったモ
デルを考え,回帰分析を実施する.
3.3.7 多重共線性
多重共線性とは,3.2節で述べた仮定Ⅶに関連したものであり,独立変数(説明変数)間の相関が
高いことである.厳密に数学的に見れば,ほとんどすべての場合において,説明変数行列Xの階数(
ランク)は k+1(すなわち,XTX は正則)であり,det(XTX)≠0となる.しかし,説明変数間の相関が
高いとき,det(XTX)は0に近い値になる.このとき,推定量bの分散が非常に大きくなってしまい,統
計的に有意な推定値が得られない.このような現象を“多重共線性”と呼ぶ.
多重共線性が存在するときには,次のことが生じる.
◆ 係数の推定値の不偏性は保たれるが,その値は極めて不正確かつ不安定になる.すなわち,推定値
の符号が理論と合わなかったり,若干のデータが追加・削除されるだけで係数の推定値が大幅に変動
することがありうる.
◆ 一般に係数の標準誤差が大きくなる(t値が小さくなる).したがって,本来は有意な変数を間違
って削除してしまう可能性が生じる.
ここでは,多重共線性の検出法としてファラーとグラウバーの方法を説明する.
データ数をn,独立変数の個数をk,独立変数の相関行列をRとしたとき,次の統計量を求める.
χ2* = -[n-1-{2(k+1)+5}/6] ln(det R)
このとき,χ2* は自由度 k(k+1)/2 の χ2 分布に従い,χ2*<χε2 であればRが直交している(多重共線
性が存在しない)という仮説は棄却できない.逆に,χ2*>χε2* であれば多重共線性が存在すると推測で
きることになる.ただし,χε2 は有意水準εでの χ2 分布の臨界値であり,一般に有意水準εとして0.95
が用いられる.多重共線性が存在するときの対処法は,ここでは割愛する.
Excelによる多重共線性の検定
まず相関行列Rを求める.ここでは図12のデータを例にして相関行列を求める方法を説明する.
図13
3.3.5 分散均一性の検定
経済・経営分野での例においては,分散の不均一性が現れる場合,たいていは分散がいずれかの説明
変数と関連をもったものとなる.そのため,分散均一性の検定方法として,説明変数を用いたものが提
案されている.ここでは,数多くある検定方法の中で,最も機械的に処理可能な方法であるゴールドフ
ェルド・クォントの方法を説明する.
【手順1】撹乱項の分散と関係があると思われる説明変数の大きさの順にデータを並べ替える.
【手順2】並べ替えたデータのちょうど中間にあるc個のデータを省く.ただし,cはデータ総数n
の1/5から1/3の範囲で残りのデータ数が偶数となるように選ばれる.
【手順3】取り除かれた残りのデータの前半の(並べ替えのキーとなった説明変数が小さい値をもつ)
データ部分と後半の(説明変数が大きい値をもつ)データ部分それぞれに回帰分析を行う.
【手順4】各回帰分析結果の残差2乗和 ESS1(前半のデータに対応した残差2乗和)と ESS2(後半の
データに対応した残差2乗和)を求める.
【手順5】撹乱項が正規分布に従い,系列相関が存在しないとき,ESS2/ESS1 は自由度 (n-c-4)/2,
(n-c-4)/2 のF分布に従う.もし計算された ESS2/ESS1 がF分布の臨界値よりも小さいときは,
選択された有意水準で帰無仮説(分散均一の仮説)が採択され,大きいときは帰無仮説が棄却さ
れ対立仮説(分散不均一の仮説)が採択される.
3.3.6 分散が不均一である場合の対処法
【手順1】本来の回帰モデルに対して最小2乗法を適用し,残差 e1,e2,・・・,en を求める.
【手順2】撹乱項の分散のおおざっぱな推定値である残差の2乗データej2と,撹乱項の分散と関係が
あると思われる説明変数データ Xij とをプロットし,両者間の関係式を推定する.関係式とし
ては,
ej2 = cXij, ej2 = cXij2, ej2 = c/Xij
などが考えられる.
【手順3】上の推定された関係式に応じて,本来の回帰モデルの両辺を,Xi1/2,Xi,Xi-1/2 で割ったモ
デルを考え,回帰分析を実施する.
3.3.7 多重共線性
多重共線性とは,3.2節で述べた仮定Ⅶに関連したものであり,独立変数(説明変数)間の相関が
高いことである.厳密に数学的に見れば,ほとんどすべての場合において,説明変数行列Xの階数(
ランク)は k+1(すなわち,XTX は正則)であり,det(XTX)≠0となる.しかし,説明変数間の相関が
高いとき,det(XTX)は0に近い値になる.このとき,推定量bの分散が非常に大きくなってしまい,統
計的に有意な推定値が得られない.このような現象を“多重共線性”と呼ぶ.
多重共線性が存在するときには,次のことが生じる.
◆ 係数の推定値の不偏性は保たれるが,その値は極めて不正確かつ不安定になる.すなわち,推定値
の符号が理論と合わなかったり,若干のデータが追加・削除されるだけで係数の推定値が大幅に変動
することがありうる.
◆ 一般に係数の標準誤差が大きくなる(t値が小さくなる).したがって,本来は有意な変数を間違
って削除してしまう可能性が生じる.
ここでは,多重共線性の検出法としてファラーとグラウバーの方法を説明する.
データ数をn,独立変数の個数をk,独立変数の相関行列をRとしたとき,次の統計量を求める.
χ2* = -[n-1-{2(k+1)+5}/6] ln(det R)
このとき,χ2* は自由度 k(k+1)/2 の χ2 分布に従い,χ2*<χε2 であればRが直交している(多重共線
性が存在しない)という仮説は棄却できない.逆に,χ2*>χε2* であれば多重共線性が存在すると推測で
きることになる.ただし,χε2 は有意水準εでの χ2 分布の臨界値であり,一般に有意水準εとして0.95
が用いられる.多重共線性が存在するときの対処法は,ここでは割愛する.
Excelによる多重共線性の検定
まず相関行列Rを求める.ここでは図12のデータを例にして相関行列を求める方法を説明する.
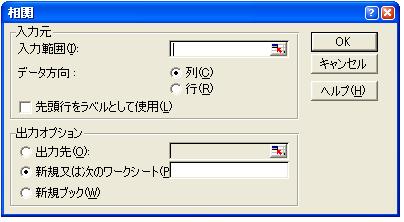 図14
回帰分析と同様に,メニューバーの【ツール】→【分析ツール】→【相関】をクリックする.すると
図14のような“相関ウイザード”が開く.そこで独立変数のデータ領域 C54:E68 を入力範囲として指
定(ドラッグ)する.このとき,各データのラベルを含めて範囲指定したので,“先頭行をラベルとし
て使用(L)”をクリックし“OK”ボタンをクリックする.新しいワークシートに図15のような計算結
果が表示される.これが相関行列であるが,相関行列は対象行列であるため,その半分しか表示されな
い.ここでの例では,空欄のセルC2,D2,D3はセルB3,B4,C4 と同じ値になる.そこで,それらの値
をコピーすることで相関行列Rが完成する.
図14
回帰分析と同様に,メニューバーの【ツール】→【分析ツール】→【相関】をクリックする.すると
図14のような“相関ウイザード”が開く.そこで独立変数のデータ領域 C54:E68 を入力範囲として指
定(ドラッグ)する.このとき,各データのラベルを含めて範囲指定したので,“先頭行をラベルとし
て使用(L)”をクリックし“OK”ボタンをクリックする.新しいワークシートに図15のような計算結
果が表示される.これが相関行列であるが,相関行列は対象行列であるため,その半分しか表示されな
い.ここでの例では,空欄のセルC2,D2,D3はセルB3,B4,C4 と同じ値になる.そこで,それらの値
をコピーすることで相関行列Rが完成する.
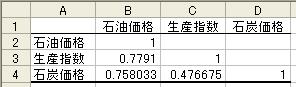 図15
得られた相関行列Rを用いてln(det R)を計算する.そのために,適当なセル(ここではB6とする)に
数式 =LN(MDETERM(B2:D4)) を入力する.結果は -1.900 となる.n=14,k=3 であるので,適当なセル
(ここではB7とする)に χ2* を求めるため,数式 =-(14-1-(2*(3+1)+5)/6)*B6 を入力する.結果は
20.58 となる.また,Excelにおいて χε2 は数式 =CHIINV(有意水準,自由度) で計算されるので,
=CHIINV(0.95,6) を適当なセルに入力すると 1.635 となり,χ2*=20.58>1.635=χ0.952 であるので多
重共線性が存在することになる.
図15
得られた相関行列Rを用いてln(det R)を計算する.そのために,適当なセル(ここではB6とする)に
数式 =LN(MDETERM(B2:D4)) を入力する.結果は -1.900 となる.n=14,k=3 であるので,適当なセル
(ここではB7とする)に χ2* を求めるため,数式 =-(14-1-(2*(3+1)+5)/6)*B6 を入力する.結果は
20.58 となる.また,Excelにおいて χε2 は数式 =CHIINV(有意水準,自由度) で計算されるので,
=CHIINV(0.95,6) を適当なセルに入力すると 1.635 となり,χ2*=20.58>1.635=χ0.952 であるので多
重共線性が存在することになる.
|