オペレーションズ・リサーチのページ

試験7月26日，自筆ノートのみ持込可能

Report

講義内容

4月12日の内容

・オペレーションズ・リサーチの問題例について説明した
・楽に単位を取る方法→授業に出てその日の内容を理解する
線形計画問題の例：鉄鋼メーカーの製品ミックス
max 10x_1  + 6x_2
s.t. 4x_1  + 2x_2 <= 24
      x_1  +  x_2 <=  8
              x_1 >=  0
              x_2 >=  0

4月19日の内容

・線形計画問題の標準化
レポート問題の解答
max   x_1  + x_2
s.t.  x_1  + x_2 >= 5
     2x_1  + x_2 >= 6
             x_1 >= 0
             x_2 >= 0
標準形 
min  -x_1  - x_2
s.t.  x_1  + x_2  - x_3       = 5
     2x_1  + x_2        - x_4 = 6
              x_1 >=  0
              x_2 >=  0
              x_3 >=  0
              x_4 >=  0
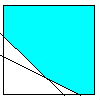　有限な解は存在しない（解は無限大）

4月26日の内容

・シンプレックス法

5月10日の内容

・最適性の条件

reportについて

ピボット軸となった基底変数の係数を１となるようにするため、式全体をその係数で割ってください。 式の意味は同じですが、形を整えるため。

5月17日の内容

・シンプレックス・タブロー

5月24日の内容

・双対問題の意味
(ノート補足）
主問題P（変数2つ，制約3つ）と双対問題D（変数3つ，制約2つ）の最終タブローにおける関係 
双対問題（変数y_i, スラック変数t_i)
 0  4 0  4  2 | 64=f
--------------+-----
 1 -3 0  1 -1 | 4
 0  7 1 -1  2 | 4
解はy_1=4, y_3=4, y_2=t_1(←第1式のslack)=t_2(←第2式のslack)=0
主問題P（変数2つ，制約3つ）の最終タブローは 
 t_1 t_2 y_1 y_2 y_3| -f
--------------------+-----
  1   0  -1   0   1 | t_1の相対コスト（左の表の中の1の場所に注目）
  0   1   1   0  -2 | t_2の相対コスト
  0   0   2   1  -7 | y_2の相対コスト

となるので，

  0   0   4   0   4 |-64
--------------------+-----
  1   0  -1   0   1 | 4
  0   1   1   0  -2 | 2
  0   0   2   1  -7 | 4
解はx_1=4, x_2=2, s_2=4　となる

reportの略解

１．双対問題 
max 5 y_1  + 3 y_2
s.t. 2y_1  +  y_2 <= 1
      y_1  + 2y_2 <= 1
              y_1 >= 0
              y_2 >= 0
２．標準形 
min -5 y_1 - 3 y_2
s.t. 2y_1  +  y_2 + y_3 = 1
      y_1  + 2y_2 + y_4 = 1
              y_1,..., y_4 >= 0
タブロー 
-5  -3  0  0  |  0
-------------------
 2   1  1  0  |  1
 1   2  0  1  |  1

0 -1/2 5/2  0 | 5/2
---------------------
1  1/2 1/2  0 | 1/2
0  3/2 -1/2 1 | 1/2

 0 0 7/3 1/3  | 1/3
--------------------
 1 0 2/3 -1/3 | 1/3
 0 1 -1/3 2/3 | 1/3

y_1 = 1/3
y_2 = 1/3
y_3 = 0
y_4 = 0

x_1 = 7/3
x_2 = 1/3

5月31日の内容

・2段階法の活用 （原点が実行可能解に含まれない時に必要）

6月7日の内容

・ネットワーク計画（最短路問題）

　例えば以下のようなネットワークの最短路はどのような問題を解けばいい？
　　枝１＝(1,2)，長さ＝2
　　枝２＝(1,3)，長さ＝5
　　枝３＝(2,4)，長さ＝6
　　枝４＝(3,4)，長さ＝2
　　枝５＝(2,3)，長さ＝1

6月14日の内容

・ネットワーク計画（最大流問題）

6月21日の内容

・ゲームと線形計画（じゃんけんゲーム)
ぐー：ちょき：ぱーを5:7:3の割合で出す混合戦略

この割合で手を決めると期待値としてゼロ歩という解を得る
（当然相手も同じように考えるから勝ち負けはつかないはず＝ゼロ和非協力ゲーム）

6月28日の内容

・ゲームと線形計画（囚人のジレンマ）

２×２の支払行列から構成される非協力ゲームはグラフを使って解くことができる
例えば

6  20
3   0
のような支払行列のとき 
min   u
s.t.  6x  +20y  - u <=  0
      3x        - u <=  0
       x  +  y       =  1
      x,y >= 0
となるがｙを消去して 
min   u
s.t.  6x  +20(1-x)  - u <=  0
      3x            - u <=  0
      x >= 0 1-x> = 0
これをグラフで解いてゲームの値を求めることができる

7月5日の内容

・ゲームと線形計画（協力ゲーム）

7月19日の予定

・Excelのソルバーを使って問題を解く
１．じゃんけんゲームを解く
２．モラを解く
参考
http://www.kogures.com/hitoshi/webtext/lp-solver/
ソルバーの使い方が説明してあります

過去問

注：過去問は今年の範囲外のところから出題されているものもあります

97年

>問２：人為問題の作り方

スラック変数をいれる 
  x_1 + 2 x_2 + x_3 - s_1 = 6
3 x_1 + 2 x_2 - x_3 + s_2 = 12
第１式のスラック変数の係数はマイナスなので初期解にできない （s_1 = -6とはできないから）
したがって人為変数を入れて補助問題を作る 
min  x_4
s.t.  x_1 + 2 x_2 + x_3 - s_1 + x_4 = 6
    3 x_1 + 2 x_2 - x_3 + s_2       = 12
    x_i, s_i >= 0

>問２：双対問題の作り方

制約第２式に-1をかけて、第１式同様「>=」の不等式にする。 （双対問題に変換する際には右辺の定数が負でもかまわない） 形をそろえた上で双対の関係にある問題に書き換える

99年

01年

問1(1) なぜ人為変数が1つ？

まずスラックを導入して 
min -2 x_1 -3 x_2
s.t.   x_1 +  x_2 - s_1 = 3
     2 x_1 +  x_2 + s_2 = 2
    x_i, s_i >= 0
この標準形の問題はs_1の係数が負なので2段階法を使わないといけない． ただし第2式はs_2の係数は正なので人為変数を入れなくてもよい． したがって補助問題は 
min    x_3
s.t.   x_1 +  x_2 - s_1 + x_3 = 3
     2 x_1 +  x_2 + s_2       = 2
    x_i, s_i >= 0
となり，第1段階のシンプレックスタブローは 
(0  0  0 0 1 | 0)
-1 -1  1 0 0 | -3
-------------+-----
 1  1 -1 0 1 | 3
 2  1  0 1 0 | 2
となる．（もちろん２つ人為変数を入れてもいいが冗長になる）

>問３：z=1/3となったが、どちらに有利なゲームなのか

目的関数の値zはAの支払期待値であるから、 それがプラスであるときはAに不利なゲームであるといえる

03年

略解

1(1) 

min  - x_1  - 2x_2
s.t.   x_1  + 3x_2  + x_3        =  3
      2x_1  + 2x_2        + x_4  =  3
      x_i >= 0
1(2)最終タブロー 
   0   0   1/2    1/4 | 9/4
----------------------+-----
   0   1   1/2   -1/4 | 3/4
   1   0  -1/2    3/4 | 3/4
1(3)双対問題 
min   3y_1    3y_2
s.t.   y_1  + 2y_2   >=  1
      3y_1  + 2y_2   >=  2
      y_i >= 0
1(4) 肥料コスト最小化問題

2(1)Aの支払行列、出す手は(1,1)(1,2)(2,1)(2,2)の４つ 

 0  2 -3  0
-2  0  0  3
 3  0  0 -4
 0 -3  4  0
2(3) 非協力ゼロ和ゲームだから

2(4) 上記支払行列の2、3列目を使う

min   z
s.t.  2x  - 3y  - z <=  0
     -3x  + 4y  - z <=  0
       x  +  y       =  1
      x,y >= 0
よりグラフで解くと x = 7/12, y = 5/12 で z = -1/12
Aに有利。Aは７：５で手を出すとよい

3(1) 2分グラフで書ける最小費用流問題。 需要点と供給点が完全に分かれている。

3(2) コストを好感度のマイナス、需要供給量を1とする． 変数xijを男iと女jがペアとなる度合いを表すとする． 

min   -3 x11 -7 x12 -2 x13 - ... -4 x33
s.t.  x11 + x12 + x13 = 1
      x21 + x22 + x23 = 1
      x31 + x32 + x33 = 1
      x11 + x21 + x31 = 1
      x12 + x22 + x32 = 1
      x13 + x23 + x33 = 1
      各xij >= 0
注：この問題の変数は必ず整数（ゼロか1）となることが知られている

■質問等何かありましたら メールか、 または研究室（2階）まで。
■3階のコンピュータルーム使えるようにしておくように